EF games and FO logic: Winning Strategies
If we take a closer look at lesson #3, we see that winning strategies for the Ehrenfeucht-Fraïssé games translate
naturally into first order logic.
In lesson #3, we described a winning strategy for the Spoiler as follows:
- There is a possible move for the Spoiler such that
forall possible answer moves of the Duplicator
there is a possible move for the Spoiler such that
forall possible answer moves of the Duplicator
...
after n rounds, the Spoiler wins
This translates into saying that:
- There exists a node in the graph A (that the Spoiler will choose as part of his winning strategy) such that
forall nodes in B (that is for any node that the Duplicator might choose in response)
there exists another node in A/B (that the Spoiler will choose) such that
forall nodes in B/A(that the Duplicator might choose)
......
some FO sentence with quantifier rank n becomes true on A, and false on B, or viceversa.
Example 1:
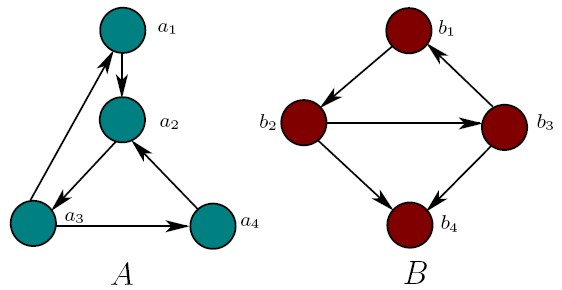
Instead of trying to guess appropriate moves for the Spoiler, let us first look
at the two graphs and try to identify a property (expressible in first oreder logic)
that only one of the graphs has. At first glance we notice that in the graph B there is one node with no outgoing edges,
namely b4, whereas in the graph A, all nodes have one outgoing edge.
So we can formulate the property that distinguishes between the two graphs by:
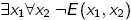
This yelds a strategy for the Spoiler to win the EF game on A, B after 2 rounds.
The spoiler picks b4 in the first round. After the Duplicator has picked some node ai in the graph A,
the Spoiler picks the node ak in A for which E(ai, ak) is true. Spoiler wins, because
Duplicator is unable to pick a node b* in B for which E(b4, b*) is true. So the Duplicator
is unable to respond in a way in which the partial isomorphism in maintained.

It is worth mentioning that the observation above is actually a theorem.
Theorem (Ehrenfeucht,Fra´ssÚ): Let A, B be two graphs. The following statements are equivalent:
- A and B satisfy the same first-order sentences of quantifier rank n.
- A~nB, i.e. the Duplicator wins the n-move Ehrenfeucht-Fra´ssÚ game on A and B
Example 2
Consider the graph depicted below. Show that:
- A~2B, i.e. the Duplicator wins the 2-move EF game on A,B
- The Spoiler wins the 3-move EF game on A,B

a. The Duplicator can win in such a way that there is an edge between x1 and x2 if and
only if there is an edge between y1 and y2, where x1 ,y1,
x2 ,y2 represent the nodes chosen in the first 2 rounds. Hence {x1,x2}
and {y1,y2} will be partially isomorphic.
b. In contrast, the Spoiler can win the 3-move game by picking three elements in B with no edge between them.
A first order sentence of quantifier rank 3 that captures this difference is:

The Spoiler wins by picking 3 nodes b
i, b
j and b
k from B for which the following
proposition is true:

Exercise: Find a different FO sentence of quantifier rank 3 that witnesses the difference between A and B.
Use it to formulate a different strategy for the Spoiler to win the 3-move EF game on A and B.