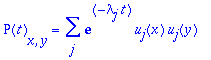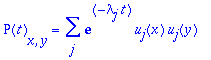Normal Derivatives on the Sierpinski Gasket
We were very interested in learning more about normal derivatives of eigenfunctions at the boundary points, especially in relation to the heat kernel. The Dirichlet heat kernel is given by this equation:
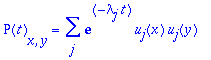
Wherein j represents a certain sequence of spectral decimation which determines lambda, lambda is the eigenvalue of u, u is a Dirichlet eigenfunction across the gasket, x and y are two interior points, and t is time. Since u is a Dirichlet eigenfunction, it vanishes at the boundary and the u's must form an orthonormal basis. Summed over all possible lambdas, we see how heat spreads from point x to point y. We were very interested in the normal derivatives, which would tell us how heat exited at a boundary point y over time when infused into a boundary point x.
Using MAPLE, I created many simple programs to graph the normal derivative of the heat kernel over time. One describes the normal derivative of the heat kernel where y=x, i.e. How heat comes back out of a boundary point when infused in that spot, and one where y is a different boundary point.
Before we begin, you will need to understand spectral decimation on the Gasket. Please read this first.
Now, let's investigate the normal derivatives of the eigenfunction. There are two different maple files, one for the 2-series and one for the 5-series. We're actually still missing many eigenvalues since the 5-series we took is one which begins on level 0, i.e. on the largest boundary points. There are entirely different serieses which occur when you start the five series on level 1 or level 2 or deeper. To run any of the files, however, you will need to first download the following m-files which contain the values of lambda and the normal derivative for j from 1 to 512. 2-series, 5-series
If you would like to see a list of all the eigenvalue and normal derivative values, you can go here.
If you've correctly downloaded these programs, you can now download and run the rest of the programs. If they did not download correctly, check the following common mistakes: 1) the file type, 2) the file location. The file's must have a ".m" ending. Some browsers try to classify them as txt files, don't let it. Also, make sure that you have downloaded the m-file to the same location as the rest of the files, or you'll need to change the path within the program itself.
Normal Derivative of the Dirichlet Eigenfunction
If that has all worked correctly, you're ready to download the first programs here: 2-series Plot Program,5-series Plot Program . These programs plot the values of the normal derivative of the dirichlet eigenfunction used in the heat kernel versus the eigenvalue for each of the first 512 j's, as you can see below. The values fall between two lines, the top having a slope of approximately .5, the bottom having a slope of approximately .317. The upper limit indicates that the normal derivative of the eigenfunction is on the order of the square root of the eigenvalue, which is exactly the case for the unit interval. This is what we would hope for, and it's good to see the data support the conjecture. The bottom limit appears random at first, but in fact is .317 is equal to one divided by the order of the Laplacian on the Sierpinski Gasket. As yet, we do not know why that should play the role of a lower bound, but hope to answer this question in the future. The programs I used to calculate the lower bound are available here: 2-series Minimum Program, 5-series Minimum Program
I created many graph close-ups to investigate the Cantor-set-like structure the graphs fall into. They can be found below in the chart, listed by which sequences they cover. All graphs are natural log graphs. The program used to create these can be found here and used to zoom in on any set of points.
Normal Derivative of the Heat Kernel at the Same Boundary Point
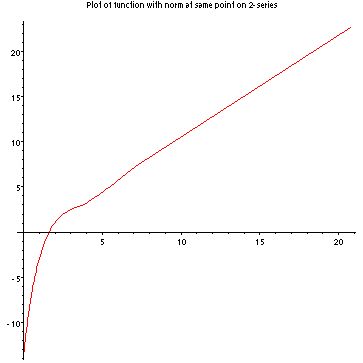
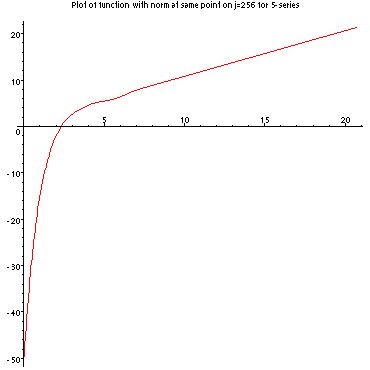
The next thing I did was to graph the normal derivative of the heat kernel over time on the gasket. Attached are two programs which will show you the graphs and allow you to find the values at specific points: 2-series, 5-series.
Here you can see what the two graphs look like for j=512.
At first glance, one might suspect that these functions were linear after a certain point. But running the programs above and checking various data points, we found that they were not linear at all, but appeared to be oscillating.
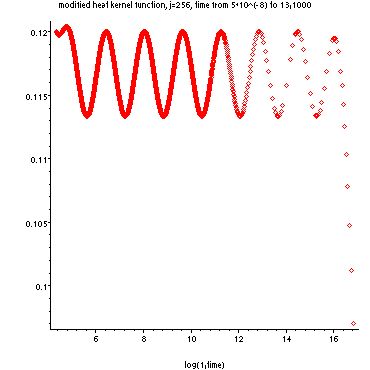
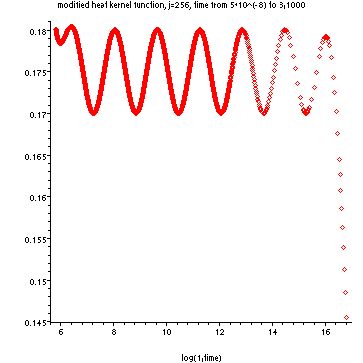
Based on previous work of Professor Strichartz's, we guessed that the normal derivative of the heat kernel was proportional to time to the -(d+2/d+1) power, where d is the order of the Sierpinski Gasket. We then multiplied the our normal derivative function by the reciprocal of this formula. If the graph was actually linear, we would see a straight line. But if it was oscillatory, we would see something sinusiodal. Below are graphs for the 2-series and 5-series, with j=256 and j=512. The programs used to create them are available here: combo2,combo5.
| 2 Series |
2 Series |
 |
 |
| 5 Series |
5 Series |
 |
 |
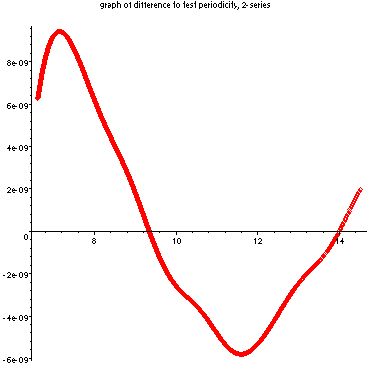
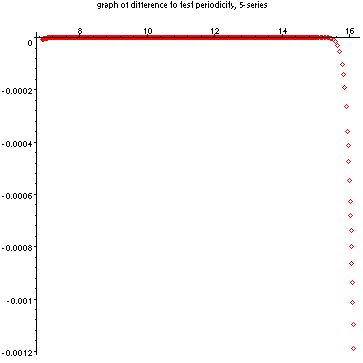
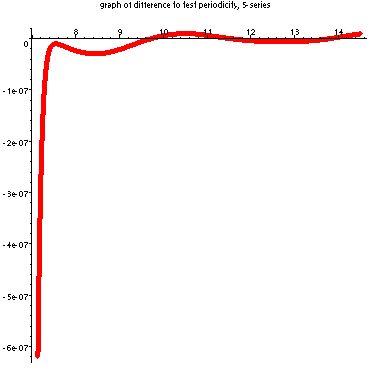
As you can see, these graphs are definitely oscillatory. The more points that are taken, the further the oscillation is maintained, so we conjecture that the oscillation continues indefinitely. We wished to investigate the periodicity of the function so I created programs which graphed the original function minus one that was shifted over by the natural log of 5. Below are the graphs of this difference.
The first two graphs are for the 2-series, and the second shows portions unaffected by roundoff errors and restrictions on terms. As you can see, the scale is incredibly small compared to the original graph, which had an amplitude of about .003.
These next graphs are for the 5-series. Again, we are slowly removing portions affected by computer limitations. Again, the scale is very small compared to the original graph, which had an amplitude near .005.
Thus, we can be fairly confident that the graphs have a period of ln(5). We are still investigating to see exactly how sinusoidal they actually are. The programs used to create these graphs and which investigate the new function are available for download here: 2-series,5-series.
Normal Derivative of the Heat Kernel at Different Boundary Points
I also investigated the normal derivative of the heat kernel when x and y where two different boundary points. This required the summing of the 2-series and 5-series. Attached is the program used to create the graph the following graph :
Diffpoints Program.
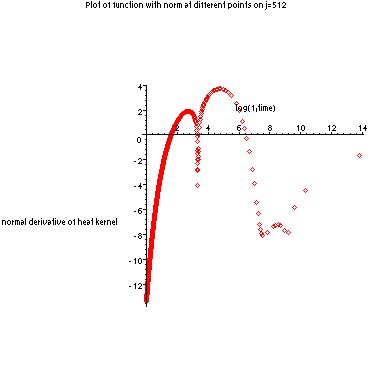
As you can see, the graph is negative mostly, except for a small portion in the middle. Since the x-axis represents the natural log of 1/time, this means that for most of the time, and permanently after t=.2006475204, the heat output is very small. The cusps in the graph represent points at which the 5-series and 2-series shift dominance. Dominance begins in the 2-series.
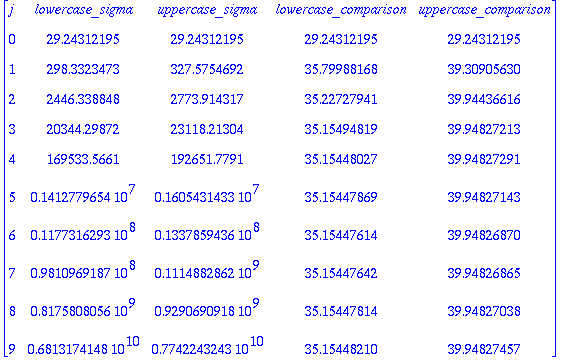
Finally, we investigated the sum of the normal derivative of the eigenfuction term in the sum only (i.e. we excluded the exponential from the sum). As it turns out, both the sum over all j's (represented by an uppercase Sigma) and the sum over the j's in each in grouping of 2^(k-1) to 2^k (represented by a lowercase sigma) grow like (25/3)^k when you take 2^k values of j. Below are the lists of values for each sigma and the ratio of each to (25/3)^k. As you can see, it quickly converges.
| 2 Series |
 |
| 5 Series |
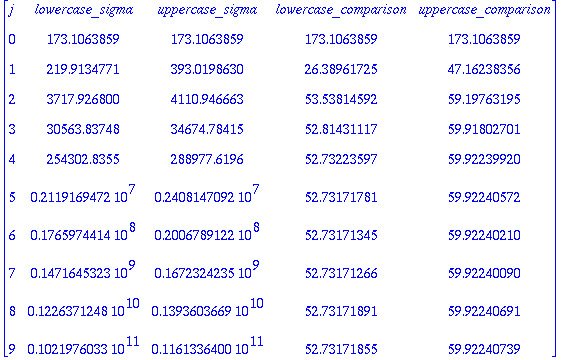 |
Also the normal derivative is bounded below by the summation over the normal direvatives only, for lambda less than or equal to 1/t if 1/t is approximately 5^k. This means that the t^-(d+2/d+1) term mentioned above equals (25/3)^k. The program used to check this is available here.
main