Comparison of three rodent cytochromes

We compare the mRNA sequences for proteins Rattus norvegicus cytochrome P450 IIA1 and IIA2, (Cyp2a1 and Cyp2a2), from [MNKG], and Mus musculus cytochrome P450, IIA12 (Cyp2a12), from [ILJN].

**Figure 1:** Comparison of cytochromes Rn-Cyp2a1 and Mm-Cyp2a12. We show the log likelihood difference $\Delta W$ in grayscale. Qualitatively, the other pairwise comparisons, with Rn-Cyp2a2, look the same. The unique sharp diagonal boundary between black and white triangles shows the best alignment, which far surpasses any alternative model.

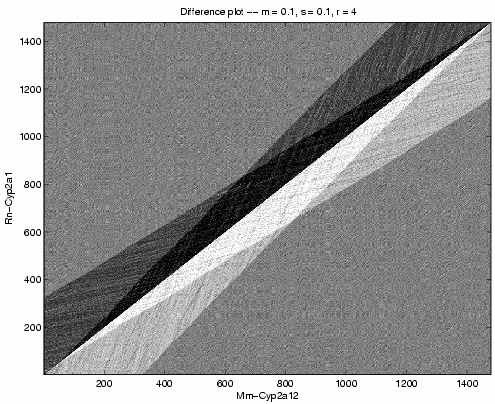
Figure 1 shows a grayscale plot $\Delta W(i,j)$ for sequences Rn-Cyp2a1 and Mm-Cyp2a12 using the parameters m = s = 0.1 and r = 4. From this picture, we can infer that the evolutionary history between these sequences contains no jump events. Thus, we set $r = \infty$ for further iterations. We also see no deletion events, so we decrease

**Figure 2:** Comparison of cytochromes Rn-Cyp2a1 and Mm-Cyp2a12, with parameters derived from the no jump, no deletion hypothesis, $r = \infty$ , decreased from figure 1. We show the log likelihood difference $\Delta W$ in grayscale.

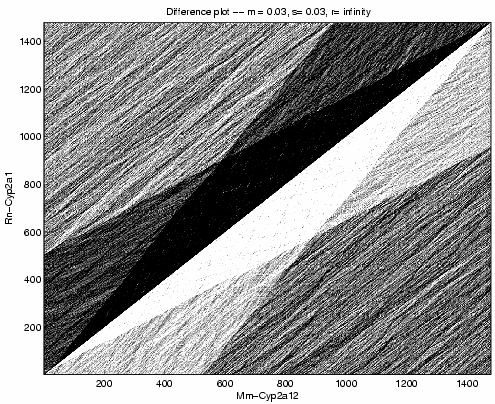
Figure 2 shows a grayscale plot of $\Delta W(i,j)$ with parameters

, $r = \infty$ . We perform this computation for all three pairs of sequences. For the following pairs, we calculated the difference between the maximum and minimum of the

array.

Mm-Cyp2a12	Rn-Cyp2a1	2263
Mm-Cyp2a12	Rn-Cyp2a2	2110
Rn-Cyp2a1	Rn-Cyp2a2	2398
Mm-Cyp2a12	Mm-Cyp2a12	2844

We expect two random sequences to be about 27% identical. The value is greater than 25%, because the distribution of nucleotides $\pi$ is not flat. We know Mm-Cyp2a12 is 100% identical to itself. By dividing 73% into 2844, we find that a difference of 38 units of log-likelihood represents 1% of sequence identity for these sequences and parameters.

Mm-Cyp2a12	Rn-Cyp2a1	14.9%
Mm-Cyp2a12	Rn-Cyp2a2	18.8%
Rn-Cyp2a1	Rn-Cyp2a2	11.4%

**Figure 3:** Phylogenetic tree for cytochromes Rn-Cyp2a1, Rn-Cyp2a2, and Mm-Cyp2a12. Reestimation of the substitution parameter with $r = \infty$ and $m = 10^{-6}$ determines the edge lengths.
$\begin{figure}\centering %% [htbp] \begin{picture}(200, 200)(0,0) \put(100,100){... ...ne(-3,-2){75}} \put(145,75){7} \put(135,37){Rn-Cyp2a2} \end{picture}\end{figure}$

We compute arrays with new parameters. We maintain $r = \infty$ . We set $m = 10^{-6}$ . We set

to be the whole number percentages near the values computed above. The plots of $\Delta W$ are similar to those for figures 1 and 2. The values of

which produce the maximum log-likelihoods are:

Mm-Cyp2a12	Rn-Cyp2a1	14%
Mm-Cyp2a12	Rn-Cyp2a2	17%
Rn-Cyp2a1	Rn-Cyp2a2	11%

Figure 3 represents these percent identities as branch lengths on an unrooted phylogenetic tree.