Lecture 2: An Introduction to Number Theory
In this lecture, we are going to discuss the first properties in the
field of number theory. These are essential for our continued study
of cryptology. We can do little more without some basic definitions
and results. Whenever possible, examples will be used to illustrate
the ideas. The hope is that this brief introduction inspires the
reader to study this beautiful field more thoroughly.
Prime Numbers
A positive integer is called a prime number if it is divisible
only by one and itself. Primes form the building blocks of all numbers
because of the following theorem.
Theorem [Fundamental Theorem of Arithmetic]:
Every positive integer is uniquely a product of prime numbers.
Of course, given a number 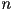 , a prime
, a prime  can appear on its list more than once. For instance, the
number
can appear on its list more than once. For instance, the
number 
Much later on, we will see that factoring a number into its prime
factors is extremely difficult and plays an important role in
cryptology. But first, we continue to study our prime numbers.
We know that there are infinitely many numbers. And we know that each
can be written uniquely as a product of primes. So it seems that
there must be quite a few prime numbers. However, is it possible that
only finitely many prime numbers could generate all of the numbers?
The answer to this question goes back to Euclid.
Theorem: There are infinitely many prime numbers.
Proof: Suppose that there were only finitely many prime
numbers. Then, we could write them all down in a list, 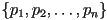 . Consider now the number
. Consider now the number

It is necessarily larger than any of the primes on our list, and so
therefore is not prime. But, from the Fundamental Theorem of
Arithmetic, it has a prime factorization. This means, in particular,
that it is divisible by one of the primes on our list. This cannot be
the case however, since our number divided by any prime on our list
give remainder 1. Thus, our list is incomplete and there are
infinitely many primes.
Greatest Common Divisors
Let  and
and 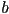 . be positive integers. By
the Fundamental Theorem of Arithmetic, both
. be positive integers. By
the Fundamental Theorem of Arithmetic, both  and
and 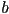 have factorizations into products of prime numbers. We
would like a way to measure how much the factorizations overlap.
Fortunately, this is easy. The greatest common divisor of
have factorizations into products of prime numbers. We
would like a way to measure how much the factorizations overlap.
Fortunately, this is easy. The greatest common divisor of  and
and 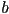 (or
(or 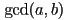 ) is
largest positive integer
) is
largest positive integer 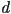 such that
such that 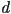 divides both
divides both  and
and 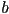 .
.
For example, 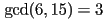 . We will see in a moment
that greatest common divisors exist for any two positive integers
. We will see in a moment
that greatest common divisors exist for any two positive integers  and
and 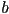 . If
. If  and
and 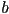 are such that
are such that  , then we say that
, then we say that  and
and 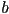 are
relatively prime. For example, 8 and 15 are relatively prime.
This terminology comes from the fact that they have no common proper
divisor other than 1; much like how a prime number has no proper
divisor other than 1.
are
relatively prime. For example, 8 and 15 are relatively prime.
This terminology comes from the fact that they have no common proper
divisor other than 1; much like how a prime number has no proper
divisor other than 1.
In particular, if  is prime, then we know that
is prime, then we know that
 is a divisor of
is a divisor of  for any
for any  . Thus we have that
. Thus we have that  . The latter case
only occurs when
. The latter case
only occurs when  is a multiple of
is a multiple of  .
.
Proposition: Given two positive integers  and
and 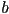 ,
, 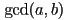 exists and is unique.
exists and is unique.
As we mentioned above, factorization is a very difficult process, so
while the above proof shows how to construct the greatest common
divisor, it is not very efficient. In the next section, we will
discuss an algorithm which works much better.
The Division Algorithm
Given two positive integers  , we can do grade school long
division to find a quotient
, we can do grade school long
division to find a quotient  and a
remainder
and a
remainder  so that we can write
so that we can write
``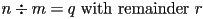 ''.
''.
Reversing this procedure shows that  . Moreover, the
long division makes sure that
. Moreover, the
long division makes sure that  , so that
, so that  and
and  we find are unique.
Amazingly, this is all we need to do to find
we find are unique.
Amazingly, this is all we need to do to find  .
.
Algorithm[The Division Algorithm]: Let  be
positive integers.
be
positive integers.
- Find
 and
and  with
with  such that
such that 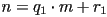 .
.
- Find
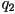 and
and 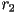 with
with  such that
such that  .
.
- Find
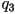 and
and  with
with  such that
such that 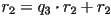 .
.
- Repeat Step 3, dividing
 by
by 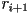 until you have a remainder of zero (i.e. until you get to
the first
until you have a remainder of zero (i.e. until you get to
the first  such that
such that  ).
).
Then, for the  where Step 4
stops, we have that
where Step 4
stops, we have that  .
.
Let's find  . We follow the algorithm
exactly:
. We follow the algorithm
exactly:
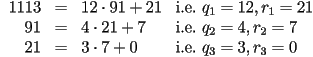
Since  , we see that
, we see that  . Indeed, one can
also check that
. Indeed, one can
also check that 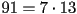 and
and 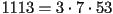 .
.
Modular Arithmetic
Recall from the last lecture that when we were assigning numbers to
represent letters or symbols, we had to 'wrap around' once we got to
the end. Accordingly, when we used the shift cipher, sometimes we had
to subtract off to make sure that our ciphertext actually made sense.
This is idea behind modular arithmetic: we fix a number 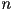 , the
modulus, and do arithmetic 'wrapping around' whenever we get
bigger than
, the
modulus, and do arithmetic 'wrapping around' whenever we get
bigger than 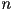 .
.
Fix our modulus to be 38. Then if we want to compute 19+25 'wrapping
around' 38, we simply find 19+25=44. Since 44>38, we need to
subtract: 44-38=6. Thus, 19+25=6 'wrapped around' 38.
Other operations work as well:
Let's now rigorously define how to do modular arithmetic, so that we
no longer need to write 'wrapped around' each time we use it! Fix a
positive integer 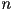 . Then we will say integers
. Then we will say integers
 and
and 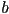 are congruent modulo
are congruent modulo
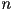 if
if 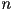 divides
divides  . In this case, we write
. In this case, we write  . We now state a
theorem which explains how usual arithmetic behaves modulo
. We now state a
theorem which explains how usual arithmetic behaves modulo 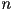 .
.
Theorem: Let 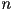 be a positive integer, and
let
be a positive integer, and
let  ,
, 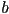 , and
, and  be any
integers.
be any
integers.
-

- If
 , then
, then 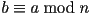 .
.
- If
 and
and 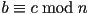 , then
, then
 .
.
- If
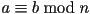 , then
, then  .
.
- If
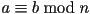 , then
, then  .
.
- If
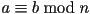 , then
, then  .
.
- If
 and
and  is
relatively prime to
is
relatively prime to 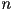 , then
, then 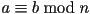 .
.
Let's re-work the previous example in our new notation.
Fix 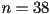
Now, let's go over a few tips for actually doing modular arithmetic.
First, if we are working modulo 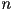 , then every number
must be congruent to one of
, then every number
must be congruent to one of  , and none of these numbers
are congruent modulo
, and none of these numbers
are congruent modulo 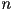 (why?). Thus, we can
automatically reduce any number to something less than our
modulus. For example, if we are working modulo 42, we can think of
156 as 30. Or, putting it in notation,
(why?). Thus, we can
automatically reduce any number to something less than our
modulus. For example, if we are working modulo 42, we can think of
156 as 30. Or, putting it in notation, 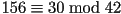 . Off
the bat, this may not seem like much of a difference, but the above
theorem shows that you can either do modular arithmetic first and then
reduce or reduce first and then do modular arithmetic. Either way will
give you the same answer! In general, it is faster to reduce first,
because it makes the numbers smaller. Let's do some examples.
. Off
the bat, this may not seem like much of a difference, but the above
theorem shows that you can either do modular arithmetic first and then
reduce or reduce first and then do modular arithmetic. Either way will
give you the same answer! In general, it is faster to reduce first,
because it makes the numbers smaller. Let's do some examples.
These are chosen to illustrate why one should reduce first, and then
do the arithmetic.
- Find
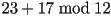 . Well,
. Well,  and
and  , so
, so  .
Alternatively,
.
Alternatively,  and
and  or
or  and
and  . Thus,
. Thus,  . But
. But 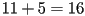 and
and  , so
, so 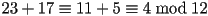 . In this case, it was one extra step to reduce first,
but it kept the numbers we worked with smaller.
. In this case, it was one extra step to reduce first,
but it kept the numbers we worked with smaller.
- Find
 . First we will do it
directly:
. First we will do it
directly:  and
and 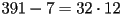 . Thus,
. Thus,
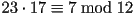 . Of course, we could have reduced first:
. Of course, we could have reduced first:  and
and  so that
so that 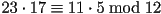 . Since
. Since  and
and  we get
again that
we get
again that 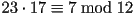 . We needed an extra step
reducing first here also, but doing so made it so all of the
arithmetic was easily done in one's head. Without reducing first, at
the minimum there was some serious paper and pencil calculation.
. We needed an extra step
reducing first here also, but doing so made it so all of the
arithmetic was easily done in one's head. Without reducing first, at
the minimum there was some serious paper and pencil calculation.
- Compute
 . In this case, it would be
much too difficult to try this directly, even with a calculator. So
our only hope is to reduce 281 modulo 23 first. Well,
. In this case, it would be
much too difficult to try this directly, even with a calculator. So
our only hope is to reduce 281 modulo 23 first. Well,  so that
so that  . Thus, we know that
. Thus, we know that  . Now, we have two options. We can either use a
calculator and compute
. Now, we have two options. We can either use a
calculator and compute 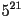 , or we can continue to
reduce modulo 23. Let's follow the second, since the first is fairly
straight forward.
, or we can continue to
reduce modulo 23. Let's follow the second, since the first is fairly
straight forward.
How do we reduce 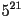 modulo 23? Notice that
modulo 23? Notice that
 . Thus, if we write
. Thus, if we write

we can see that
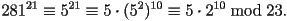
Now we work the same trick again. Since  , we have
that
, we have
that 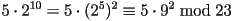 . Since
. Since  , we can rewrite this as
, we can rewrite this as  . We notice, however, that
. We notice, however, that  . Thus,
we are left with
. Thus,
we are left with 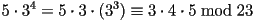 . Now,
. Now,  and
and  . Thus we conclude that
. Thus we conclude that  (Phew!).
(Phew!).
Exercises
- If any of part of this section was unclear, head to the references
section and find an introductory book on number theory. Read it. Do
the exercises.
- Pick two two-digit numbers. Find their greatest common divisor. Pick
two three-digit numbers. Find their greatest common divisor. Pick
one three-digit number and one five-digit number. Find their greatest
common divisor. Repeat this as many times as it takes until you are
comfortable finding greatest common divisors.
- Do the following modular arithmetic:
This work was made possible through a grant from the National
Science Foundation.
![]() , a prime
, a prime ![]() can appear on its list more than once. For instance, the
number
can appear on its list more than once. For instance, the
number ![]()
![]() . Consider now the number
. Consider now the number
![]()
![]() . We will see in a moment
that greatest common divisors exist for any two positive integers
. We will see in a moment
that greatest common divisors exist for any two positive integers ![]() and
and ![]() . If
. If ![]() and
and ![]() are such that
are such that ![]() , then we say that
, then we say that ![]() and
and ![]() are
relatively prime. For example, 8 and 15 are relatively prime.
This terminology comes from the fact that they have no common proper
divisor other than 1; much like how a prime number has no proper
divisor other than 1.
are
relatively prime. For example, 8 and 15 are relatively prime.
This terminology comes from the fact that they have no common proper
divisor other than 1; much like how a prime number has no proper
divisor other than 1.
![]() is prime, then we know that
is prime, then we know that
![]() is a divisor of
is a divisor of ![]() for any
for any ![]() . Thus we have that
. Thus we have that ![]() . The latter case
only occurs when
. The latter case
only occurs when ![]() is a multiple of
is a multiple of ![]() .
.
![]() and
and ![]() ,
, ![]() exists and is unique.
exists and is unique.
![]() ''.
''.
![]() . Moreover, the
long division makes sure that
. Moreover, the
long division makes sure that ![]() , so that
, so that ![]() and
and ![]() we find are unique.
Amazingly, this is all we need to do to find
we find are unique.
Amazingly, this is all we need to do to find ![]() .
.
![]() be
positive integers.
be
positive integers.
![]() . We follow the algorithm
exactly:
. We follow the algorithm
exactly:
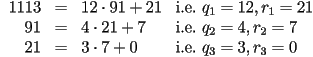
![]() , we see that
, we see that ![]() . Indeed, one can
also check that
. Indeed, one can
also check that ![]() and
and ![]() .
.
![]() be a positive integer, and
let
be a positive integer, and
let ![]() ,
, ![]() , and
, and ![]() be any
integers.
be any
integers.
![]()
![]() modulo 23? Notice that
modulo 23? Notice that
![]() . Thus, if we write
. Thus, if we write
![]()
![]()
![]() , we have
that
, we have
that ![]() . Since
. Since ![]() , we can rewrite this as
, we can rewrite this as ![]() . We notice, however, that
. We notice, however, that ![]() . Thus,
we are left with
. Thus,
we are left with ![]() . Now,
. Now, ![]() and
and ![]() . Thus we conclude that
. Thus we conclude that ![]() (Phew!).
(Phew!).