

Using this, we can take a message and associate to it a string of numbers. Then we decided that the shift cipher corresponded to adding a predetermined number to each element of the string. Of course, this wasn't exact addition. We had to `wrap around' so that every number would make sense. Then, in Lecture 2, we learned how to describe `wrapping around' mathematically through modular arithmetic. That is, we were working modulo 41. Thus, if we use a shift cipher with a shift of 14, this corresponds to finding
![]()
where ![]() denotes the plaintext we
wish to encrypt. Suppose then that this yields the ciphertext
denotes the plaintext we
wish to encrypt. Suppose then that this yields the ciphertext ![]() . To decrypt, we simply compute
. To decrypt, we simply compute
![]()
that is the shift cipher.
CAN YOU PLEASE PICK UP SOME CHIPS AND SALSA? ALICE.This message has 42 characters, so let's group it in blocks of size 3:
CAN YOU PLE ASE PIC KUP SOM ECH IPS AND SAL SA? ALI CE.Now, when we convert to numbers, we will have blocks of size 6:
030114 251521 161205 012005 160903 112116 191513 050308 091619 011404 190112 190139 011209 030537Now, the largest of these 6-digit numbers is 251521. So any modulus larger than that will work. For ease, let's choose 300000. Now, we also need to pick a shift. Say 200000. Now, to get our cipher text, we take
![]()
where ![]() is any of the six digit blocks we have
above. This yields
is any of the six digit blocks we have
above. This yields
230114 151521 061205 212005 060903 312116 091513 250308 291619 211404 090112 090139 211209 230537for our ciphertext. Also, we can now drop any leading zero's that we have since Bob will know to add them back in. This is not that big a deal, but it might trick an attacker into thinking that we haven't used a uniform block size! Thus, the final ciphertext is
230114 151521 61205 212005 60903 312116 91513 250308 291619 211404 90112 90139 211209 230537and Bob can easily recover it, so long has he knows that we shifted by 200000 and that we were working modulo 300000.
Suppose we have some plaintext ![]() , a modulus
, a modulus
![]() , and an integer
, and an integer ![]() . Then, by computing
. Then, by computing
![]()
we could generate ciphertext ![]() . This is essentially the
multiplication cipher. However, there is one issue which we have yet
to discuss: how do we decrypt the cipher text? In other words, how do
we undo modular multiplication? The answer, of course, is modular
division. Before we start on the theory, let's look at an example.
. This is essentially the
multiplication cipher. However, there is one issue which we have yet
to discuss: how do we decrypt the cipher text? In other words, how do
we undo modular multiplication? The answer, of course, is modular
division. Before we start on the theory, let's look at an example.
Suppose Carol wants to use the multiplication cipher with ![]() and
and
![]() to send Dave the following message:
to send Dave the following message:
SHOULD WE DRESS UP? CAROL.As usual, she breaks this up into blocks,
SH OU LD WE DR ES SU P? CA RO L.and then converts to numbers:
1908 1521 1204 2305 0418 0519 1921 1639 0301 1815 1237Now, she multiplies each block by
5724 4563 3612 6915 1254 1557 5763 4917 0903 5445 3711and then reduces modulo
724 2063 1112 1915 1254 1557 763 2417 903 445 1211Now, Dave must decrypt this message. Of course, he knows that
![]()
so that if
![]()
then

Thus, to 'undo' multiplication by ![]() modulo
modulo ![]() ,
we multiply by
,
we multiply by ![]() . The notation '
. The notation '![]() '
is to denote that 3 and 1667 are inverses modulo 2500. Much
like in the usual case where the inverse of 7 is
'
is to denote that 3 and 1667 are inverses modulo 2500. Much
like in the usual case where the inverse of 7 is ![]() .
Returning to our example. Having received the encrypted message, Dave
finds
.
Returning to our example. Having received the encrypted message, Dave
finds ![]() and computes
and computes ![]() ,
,
1206908 3439021 1853704 3192305 2090418 2595519 1271921 4029139 1505301 741815 2018737and then reduces modulo
1908 1521 1204 2305 418 519 1921 1639 301 1815 1237This is exactly the message which Carol sent!
From this example, it looks like all we need to do to decrypt the
multiplication cipher is determine ![]() modulo
modulo ![]() .
However, what if we had chosen
.
However, what if we had chosen ![]() instead of
instead of ![]() in
the previous example? In that case, we would have run into some
problems. Since
in
the previous example? In that case, we would have run into some
problems. Since ![]() , we call
2 a zero divisor modulo 2500. To see why this means that 2
cannot have an inverse, suppose that it did. Then we would be able to
find some number
, we call
2 a zero divisor modulo 2500. To see why this means that 2
cannot have an inverse, suppose that it did. Then we would be able to
find some number ![]() such that
such that ![]() . Then, combining the last two congruences, we would have
. Then, combining the last two congruences, we would have

Of course, we know that ![]() , so our
assumption that 2 was invertible modulo 2500 was false.
, so our
assumption that 2 was invertible modulo 2500 was false.
Let's consider the general case. Suppose we have a modulus
![]() and want to know whether or not a number
and want to know whether or not a number ![]() is invertible modulo
is invertible modulo ![]() . Suppose first that
. Suppose first that ![]() is a multiple of
is a multiple of ![]() and
and ![]() exists. That is,
suppose that there is some
exists. That is,
suppose that there is some ![]() such that
such that ![]() is a multiple of
is a multiple of ![]() and there is some
and there is some ![]() such that
such that ![]() . Then, just as in
the example, we get
. Then, just as in
the example, we get

Since ![]() and
and ![]() , we are
left to conclude that
, we are
left to conclude that ![]() and
and ![]() . Thus, the
numbers 1 < c \leq n which have a common factor with
. Thus, the
numbers 1 < c \leq n which have a common factor with
![]() are not invertible modulo
are not invertible modulo ![]() . These are precisely
the same
. These are precisely
the same ![]() which satisfy
which satisfy ![]() , or
equivalently, those
, or
equivalently, those ![]() which are not relatively prime
to
which are not relatively prime
to ![]() . The following theorem shows that the converse is also
true.
. The following theorem shows that the converse is also
true.
Theorem: Let ![]() be a positive integer and
be a positive integer and ![]() any integer. Then
any integer. Then ![]() is invertible modulo
is invertible modulo ![]() if and
only if
if and
only if ![]() and
and ![]() are relatively prime.
are relatively prime.
Now suppose that we have chosen ![]() and
and ![]() which are
relatively prime. How do we go about finding
which are
relatively prime. How do we go about finding ![]() modulo
modulo
![]() ? This requires the division algorithm discussed in Lecture
2. As usual, we will start with an example.
Suppose we want to find the inverse of
? This requires the division algorithm discussed in Lecture
2. As usual, we will start with an example.
Suppose we want to find the inverse of ![]() modulo
modulo
![]() . We start by doing the Division algorithm to make sure
that
. We start by doing the Division algorithm to make sure
that ![]() :
:
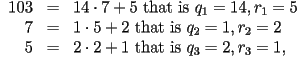
so we do in fact, have ![]() . Now, to find
. Now, to find
![]() , we simply reverse the division algorithm and
work from the bottom up:
, we simply reverse the division algorithm and
work from the bottom up:

Since ![]() , we see that
, we see that
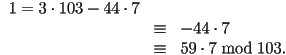
That is, ![]() . This process works in complete
generality.
Now that we can compute inverses modulo
. This process works in complete
generality.
Now that we can compute inverses modulo ![]() , we can fully use the
multiplication cipher.
, we can fully use the
multiplication cipher.
Suppose Alice wants to send the following message to Bob using the
exponential cipher with ![]() and
and ![]() :
:
TOMORROW IS THE BIG DAY! ALICE.Since exponentiating gets very large, very fast, we are going to group one letter at a time when we convert to numbers:
20 15 13 15 18 18 15 23 09 19 20 08 05 02 09 07 04 01 25 38 01 12 09 03 05 37Next, we cube each of these numbers,
8000 3375 2197 3375 5832 5832 1728 12167 729 6859 8000 512 125 8 729 343 64 1 15625 54872 1 1728 729 27 125 50653and reduce modulo
5 13 25 13 10 10 6 31 32 12 5 20 28 32 15 23 1 4 14 1 6 32 27 2 18Before we can discuss how to decrypt this message, we need some more terminology. For a given positive integer
Theorem Let ![]() and
and ![]() be positive integers
which are relatively prime. Then
be positive integers
which are relatively prime. Then ![]() . If
. If ![]() is prime and
is prime and ![]() is a positive integer, then
is a positive integer, then ![]() . In
particular, if
. In
particular, if ![]() , then
, then ![]() , and if
, and if
![]() and
and ![]() are prime, then
are prime, then ![]() .
.
The next theorem relates ![]() to exponentials. It is due to
17th century French Mathematician Pierre de Fermat.
to exponentials. It is due to
17th century French Mathematician Pierre de Fermat.
Theorem[Fermat's Little Theorem]: Let ![]() be a positive
integer. Then for any integer
be a positive
integer. Then for any integer ![]() relatively prime to
relatively prime to
![]() ,
,
![]()
Thus, if we want to decrypt a message ![]() that has be encrypted using an exponential cipher,
all we need to do is find
that has be encrypted using an exponential cipher,
all we need to do is find ![]() . Indeed,
we could then compute
. Indeed,
we could then compute

So, to decrypt our example above, Bob would need to compute
![]() , that is,
, that is, ![]() . To do this, all he needs to do is the division algorithm in
reverse!
. To do this, all he needs to do is the division algorithm in
reverse!
Before, we finish, let's think for a minute about how careful we need
to be when we are choosing ![]() and
and ![]() for an
exponential cipher. To start, we are going to insist that
for an
exponential cipher. To start, we are going to insist that ![]() is either prime, or the product of two prime numbers. In the latter
case, say
is either prime, or the product of two prime numbers. In the latter
case, say ![]() . Using the theorem about the behavior of
. Using the theorem about the behavior of
![]() , we see that the
, we see that the ![]() we choose must be
relatively prime to
we choose must be
relatively prime to ![]() . In particular, it
cannot be even (why?). If we follow these two rules, everything will
work as planned.
. In particular, it
cannot be even (why?). If we follow these two rules, everything will
work as planned.