Following are
examples and applications that have been collected from the internet,
clipped, adjusted and/or rewritten to suit our needs and notations.
Nothing is original in here, but the author believes that the
situations described were interesting enough to be included here. All
of these exercises are probably better carried on with the aid of a
computer or a graphing calculator.
1. Amusement Park
An amusement park has five adult attractions: Roller coaster, Flume,
Wheel, Smasher and Crunch. Two of these, the exciting Roller coaster
and Flume, are usually the last attractions visited before people leave
the park. There is a path between the Roller coaster and Flume, Roller
coaster
and Wheel, Roller coaster and Smasher, Flume and Wheel, Flume and
Crunch, Smasher and Wheel, and Wheel and Crunch.
Question
Assuming that people are equally likely to take any path
leaving an attraction and that 25% of the people who ride the Roller
coaster or the Flume then leave the park, draw the graph that shows the
five attractions and the exit and shows the probability that someone at
one vertex goes to any other vertex. Use E for exit, R for roller
coaster and so on. Assume that someone who has exited the park does not
return.
Question
From this graph, write the transition probability matrix P for
going from one attraction to another. The entries in column E would be
0 everywhere except at row E to indicate that someone who exits the
park does not return (”stays out”).
Question
Use this matrix to determine the probability that a person who
rides the Roller Coaster rides it once again after four changes of
rides. To do this, you need to create an initial state vector q with
zeroes everywhere expect at row R indicating you started on the Roller
Coaster. Multiply P
and q to
determine the probability distribution for
the next ride. Keep multiplying by P
to get subsequent observations.
Question
What is the probability that someone who is now riding the
Roller Coaster rides the Wheel after changing rides four times?
Question
Find the expected number of times that someone who is now
riding the Roller Coaster rides the Wheel before leaving the park.
Question
Find the expected number of rides that a person who is now
riding the roller coaster rides on any ride whatsoever before leaving
the park.
2. Genetics
A given plant species has
red,
pink,
or
white
flowers according to the
genotypes RR, RW, and WW respectively. If each genotype is crossed
with a pink flowering plant (genotype RW), the transition matrix is as
follows:
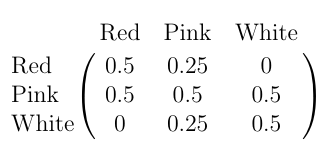
These numbers are determined as follows:
- RR x RW yields RR, RW, RR, and RW.
- RW x RW yields RR, RW, WR, WW.
- WW x RW yields WR, WW, WR, and WW.
Assume the plants of each generation are crossed only with pink plants
to produce the next generation.
Question
This is the transition matrix is P.
Now create a state vector
q
indicating an initial distribution of genotypes of 70% Red, 10% Pink,
and 20% White.
Question
Determine the distribution of phenotypes for the next generation
starting from q.
Multiply the answer with P
and keep
multiplying. Eventually the matrix product will stabilize. What
does
this show? What will be the eventual distribution of genotypes after
many generations?
Question
Suppose the initial distribution is different. Modify the values in
vector q
to indicate a different distribution (remember the
three numbers must add up to 1) and repeat the multiplications as in
the previous question. Explain your results.
Question
Suppose we decide to cross plants of each generation with only
white plants. Create a transition matrix for this situation. (To figure
the probabilities, recall that RR x WW yields RW all the time.
Calculate the other probabilities.) Use the same initial distribution
of genotypes and determine the eventual distribution after many
generations.
3. Predicting the Weather
Suppose a weather forecaster has collected data to predict whether
tomorrow will be
sunny
(S),
cloudy
(C), or
rainy
(R), given today’s
weather conditions. Here is a summary of his analysis:
- If today is sunny, then tomorrow’s
probabilities are 70% for S, 20% for C, and 10% for R.
- If today is cloudy, then the probabilities for
tomorrow are 30% for S, 60% for C, and 10% for R.
- If today is cloudy, then the probabilities for
tomorrow are 25% for S, 20% for C, and 55% for R.
Question
With this information form a Markov chain describing the
weather changes. Take as states the kinds of weather S, C, and R. From
the above information determine the transition probabilities:
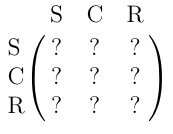
Question
Start with today’s weather and determine the probabilities for
tomorrow’s weather. Multiply by the transition matrix P again to
determine the weather for 2 days from now. Repeat this so that you have
a
set of probabilities for the next 5 days.
Question
Keep multiplying by P.
Eventually the matrix product will
stabilize. What does this show?
Question
Question Change today’s weather to
indicate a rainy day. Repeat the multiplications as before to formulate
a 5-day forecast.
Question
Now forget about state vectors and just take P and raise it to
some power, such as 20. What do you see? What does that tell you about
the significance the state vector here? For what value of n does Pn
stabilize? Once it stabilizes it no longer forecasts the weather, but
rather tells you about the climate.
Question
Question Create a matrix that would
be appropriate for Ithaca, NY. You may want to include snow as well as
rain. Decide on today’s weather and illustrate a 5-day forecast.
4. Predicting the Weather: The Land of Oz
According to Kemeny, Snell, and Thompson, the Land of Oz is blessed by
many things, but not by good weather. They never have two nice days in
a row. If they have a nice day, they are just as likely to have snow as
rain the next day. If they have snow or rain, they have an even chance
of having the same the next day. If there is change from snow or rain,
only half of the time is this a change to a nice day.
Question
With this information form a Markov chain describing the
weather changes. Take as states the kinds of weather R, N, and S. From
the above information determine the transition probabilities:
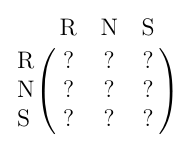
Question
Study the climate of the Land of Oz. If you don’t understand
this question, make sure you read the previous example.