Little Ricky
is a mouse and she lives in a small maze where she likes to wander from
room to room. The layout of her living space is depicted in figure 1.
Every thirty minutes or so she likes to change rooms and just moves to
one of the rooms adjacent to the one she is in at that moment. For
example, from room number 1, she might decide to move on to rooms
number 2, 4 or 5, but she wouldn’t go all the way to room 3. She is a
lazy rodent after all.
A careful study of her habits shows that the room she decides to go to
next does not depend on any kind of history. She just seems to pick one
the rooms she has access to (excluding her current location) randomly,
where each accessible room is equally likely to be chosen.
In this setting, given an initial room
i for the mouse to
be in –
i
can
be equal to 1, 2, 3, 4 or 5 – and for each other room
j , there is a
well defined number that represents the probability for the mouse to
move from room
i
to room
j.
Notice that this number does not depend on the time at which we
evaluate that probability nor does it depend on what other rooms the
mouse
visited before that.
Definition
If the mouse is
inside room i,
we will say it
is in the
state i.
We then define the transition
probability pji to be the
probability for the mouse to move to room j if she starts in
room i.
For example, here
p21
= 1/3 being the probability for the mouse to go
from room 1 to room 2: she has access to 3 rooms (2, 4 and 5) all of
which are equally likely, hence the value 1/3.
In our example, she
can’t stay in the same room more than 30 minutes, so
p11
= 0 for
example, meaning that the probability that she stays in room 1 starting
in room 1 is 0.
Question
Find all the transition probabilities pji for
and i and j
ranging from 1 to 5.
Question
What can you say about the sum p21
+ p41
+ p51
? Is this a
surprise? How about p12+
p15+
p14?
Can you explain these results?
Remember that if Ω = {ω
1, ..., ω
n
} is probability model, where the
ωi
’s
are the possible future events or outcomes, and if
pi
is the
probability of the event
ωi
occurring, then
p1
+
p2
+ ...
+
pn
=.
This just says that the sum of all probabilities is equal to on, as
something
has to happen.
For example the mouse deciding to move from room 1 to room 2 is one of
the outcomes in the probability model describing the mouse in room 1,
and its probability is 1/3 as calculated before.
2.
Steps and Probabilities
Let us put
Little Ricky back into room number 1 and watch what happens.
After about 30 minutes, she moves to another room. This could be room
2, room 4 or room 5.
After yet another 30 minutes, she moves again to one of the adjacent
rooms, and so on. For example, she might decide to move on to room 2
and then to room 3. But she might also want to come back to room 1
after she visits room 2.
Question
Suppose Little
Ricky starts in room 1 and then moves to room 2. What is
the probability of her returning to room 1 next time
she
moves? Remember that we assumed that she moved from to room
independently of any kind of history and always following the
transition
probabilities that we defined earlier.
Question
Suppose she
first moves to room 5, instead of 2. What is now the
probability of her returning to room 1 at the next step?
Question
Starting from
room number 1 now. Can you calculate the probability of her returning
to that room after 2 steps? How about
after 3?
Let us try and solve this problem for 2 steps. To simplify the
notation, we will write
R0
to denote the room she is in at the
beginning of the experiment,
R1
to denote the room she first moves to,
an so on. In this language we are trying to calculate the probability
of {
R0
= 1
and
R2
=
1}. Call this event
X
Now this event can be broken apart into 3 events depending on where she
first moves to:
A
= {
R0
= 1
and
R1
= 2
and
R2
=
1},
B = {
R0
= 1 and
R1
= 4 and
R2
= 1 } and
C
= {
R0
= 1
and
R1
= 5
and
R2
=
1}. By broken
apart we mean that in our probability model the event
X is equivalent
to
A or
B or
C . Mathematically,
this means:
X
= A ∪ B ∪ C
In
general, calculating the probability
P(
A ∪
B) of
A or
B happening
is given by
P(
A ∪
B) =
P(A) +
P(B) −
P(
A ∩
B), where the last
term
is the probability of both
A
and
B
happening. But when
A
and
B are
disjoint,
meaning they can not happen at the same time, this
probability simply becomes
P(A)
+
P(B). In
our case, the mouse can’t
be in both rooms 2 and 4 after the first step, for example. The events
A,
B
and
C and
are all
mutually
disjoint, and thus we get:
P(X
) = P(A)
+ P(B) + P(C )
While moving from one value to calculate to three may seem like making
the problem only harder, it is the very opposite in reality. Let us
look at
P(A),
for example.
The event
A
occurs when Little Ricky first moves to room number 2, and
then to room number 1 again. The probability of
A occurring is thus
the
probability of her moving from room 1 to room 2 at the first move, and
from room 2 to room 1 at the second one.
Now remember that we assumed that she moved from room to room
independently of any kind of history. This means that her moving from
room 1 to room 2 at first, and her moving from room 2 to room 1 at the
second step are
two
independent events. Probability theory tells us
that in a case like this, where Y and Z are two independent events, the
probability of both Y and Z happening is simply the product of their
probabilities, that is to say
P(Y
∩ Z) =
P(Y)
∗
P(Z).
Putting everything together, we get
P(A) =
P(moving from room
1 to
room 2 at step 1) ∗
P(moving
from room 2 to room 1 at step 2).
Remembering that those probabilities do not depend on the time and
are the transition probabilities
pij
this simplifies to:
P(A) = p12
∗
p21
Question
Carry the same process and show that P(B) = p14 p41
and that a
similar
expression holds for P(C
).
We have now shown that:
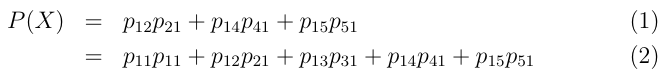
You might now be able to guess the probability of Little Ricky ending
up in room 2 after 2 steps, say. Indeed, just break that even apart
depending on what room she first moves 2, then calculate the 3
probabilities using the same principles we used in the previous
example.
Question
Calculate the probability of Little Ricky
ending up in room 2 after 2 steps starting from room 1.
Question
How about the probability of ending up in room
2 starting from 1 after 3 steps? 4 steps? n steps?
While you should be able to carry on this analysis in theory, the
calculations might quickly get out of control in practice. The
framework we will introduce in the next section will help solve that
problem and make a lot of these calculations much simpler, so that they
can even ben carried on by a computer or graphing calculator. This is
only a hint of why the Markov chain framework is so popular. Before we
do that, we dedicate the next subsection to introducing another
important concept.
3.
States of Mice
Suppose we
first flip a coin then put Little Ricky in room 1 or 2
depending on what the outcome is. For example, we put Little Ricky in
room 1 if the coin lands on tails and in room 2 otherwise. One might
wonder what the probability of Little Ricky ending up in room 5 after 1
step would be, and we will show to find that out. We assume that the
coin is fair so that both side are equally likely to come out, with a
probability of 1/2 , and that the coin and the mouse are ”independent”
of one another.
Let then
X
be the event ”she ends up in 5 after 1 step”, then following
the same kind of analysis we did earlier, we can break this event apart
into two events:
A
= {she ends up in 5 starting from 1} and
B = {she
ends up in 5 starting in 2}.
Question
Explain why P(X)
= P(A) + P(B). Now the
event A is equivalent to {She moves from 1 to 5} and {The coin landed
on tail}.
Question
Show that P(A)
= (1/2) p15
. Remember that the
mouse and the coin are independent.
Question
Conclude that P(X)
= (1/2) p51
+ (1/2) p52
Let us now assume that we roll an unfair 5-sided die such that the side
i comes out the probability
qi
. We do not assume the die to be fair,
so we do not require
q1
=
q2 = ...
=
q5 . On
the other hand, the qi
are probability values so they are all non-negative and satisfy
q1 +
q2
+ ... +
q5
= 1.
Suppose we roll the die and drop Little Ricky in the room whose number
comes out. In other words, she might be dropped in room 1 with
probability
q1,
or in room 2 with probability
q2,
and so on.
Question
What is the probability of her ending up in
room 5 after 0 steps?
Question
What is the probability of her ending up in
room 5 after 1 step? To answer this question, break this event apart
again depending
on where she is dropped first. You should get
p51 q1 + p52 q2 +
p53 q3
+ p54 q4 + p55 q5
(3)
Question
Can you do the same calculation for 2 steps?
Use what we’ve calculated earlier.