So far, given
a process modeled as a Markov chain, we are able to calculate the
various probabilities of jumping from one state to another in a certain
given number of steps. This was given by taking successive powers of
the transition matrix and reading a coefficient in the result matrix.
For example, we are to able to calculate the probability for Little
Ricky to reach state 5 in 2 steps starting in state 1, or in 3 steps
starting in 1, or even in 4 steps starting in 1.
What we are still lacking though, is the ability to answer questions
like this: forgetting about how many steps it takes her to do it, what
is the probability for Little Ricky to ever reach state 5 starting in
state 1? While it might be possible to guess what the answer should be
in this case, more complicated examples might require a new kind of
approach and this is what we will focus in this section. Rather than
giving a general statement we develop the idea using a simple example.
Let us create a new maze by describing it using the following graph:
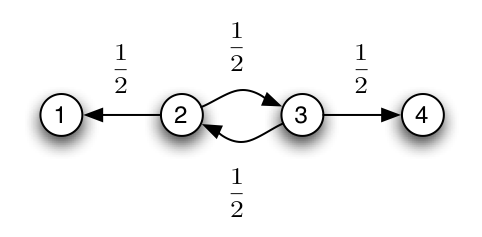
The missing arrows indicate a zero transition probability. For example,
state 1 and 4 don’t have any arrows coming out them. We call such
states
absorbing states.
This simply means once the process reaches one
of those states, it stays in them forever. In this example, rooms 1 and
4 are two exits. Once Little Ricky leaves the maze, she stays ”out”
forever – or till the end of the experiment, that is. Non-absorping
states are also called
transient.
In the following, we show how to calculate the average time it takes
Little Ricky to get to one of the exits (rooms 1 and 4) and the
probability that she exists through room 4. More precisely:
Definition
Define πi to be the probability of ever reaching state 4
starting for state i, and τi to be the average number of steps required
to get from state i to either state 4 or state 1. Finally, we will
write {i → j }
to denote the event {Little Ricky reaches state j
starting from state i}.
1. Absorption Probabilities
Let us first focus on
πi
’s. Clearly,
π1
= 0 as she can’t reach state 4
starting from state 1. Also
τ1
= 0 as 1 is one of the target states: it
takes Little Ricky no steps to get from 1 to either 1 or 4.
Question
Find π4
and τ4.
Now suppose she starts in state 2. We break the event {2 → 4} apart
depending on whether she first jumps to state 1 or 3. These two events
being disjoints, we get that:
P ( {2 → 4}) = P ({2 → 4} ∩ {She
first moves to 1}) + P ( {2 → 4} ∩
{She first moves to 3})
We first simplify this into:
P ( {2 → 4}) = P ({1 → 4} ∩ {She
first moves to 1}) + P ( {3 → 4} ∩
{She first moves to 3})
Finally, using the transition probabilities and the independence of the
transitions in a Markov chain, this becomes:
π2 = p12 π1 + p32 π3 = (1/2) π1 + (1/2) π3 = (1/2) π3
Question
Show that π3
= (1/2) π2
+ (1/2) π4
= (1/2) π2
+ (1/2)
Question
Using the two previous identities, find π2
and π3.
Question
Compare π3
and p43
.
Can you explain this result?
2. Average Time to
Absorption
To calculate the average time to
absorption we need to remember that in
probability theory, the average of a
random variable is
defined as the
expectation
of that variable:
Definition
The
expectation
of random variable X that can take values 1,
2, … ,
k
(
k can be
infinity, but mathematical care is needed to is
defined the sum) as

Getting back to our original problem, we want to calculate the average
time to get to rooms 1 or 4.
Let us write
P (i → E
in k) for the probability of reaching state 1 or
4 in
k
steps starting from state
i
and let us try to find an expression
for the average time
τ2
it takes Little Ricky to find one of the exits
starting in room 2. By the definition, we have:
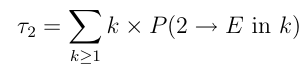
Here again, we split those probabilities depending on whether the first
step is a step towards state 1 or 3, and use the same kind of trick we
used many times before:
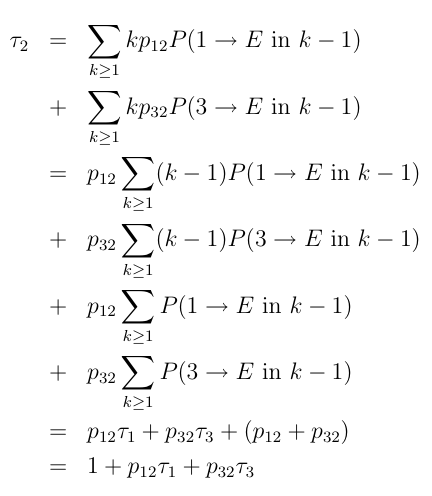
Question
Conclude that the following identity holds in our example:
τ2
= 1 + (1/2) τ1
+ (1/2) τ3
=
1 + (1/2) τ3
Question
Using a similar derivation or working by analogy, show that
the following holds:
τ3
= 1 + (1/2) τ2
+ (1/2) τ4
= 1 + (1/2) τ2
Question
Putting everything together, calculate the values of τ1
, τ2
,
τ3
and τ4.
In this section we tried to show how one can solve absorption problems
explicitly when the graph of the Markov chain is small enough to make
the calculations feasible by hand. A more general treatment of this
kind of problems requires tools from
linear
algebra beyond the scope of this introduction.