Mathematics and Sudokus: How many clues?
In the last section, we counted ways of completing an empty Sudoku puzzle. Suppose your best friend gives you a self-made Sudoku puzzle like the following one.

After a while of staring at it and not getting anywhere, you might wonder if the puzzle “actually has a solution” (what do we mean by that anyway?). It would be nice to know answers to the following questions: is there an easy way to decide if there is more than one way of completing the grid? Is there an easy way to decide if it is possible to complete a given grid?
The answer is disappointing. In general, it is very hard to decide (without the use of a computer) if a Sudoku puzzle has a solution, and if there are several ways of completing a partially filled-in grid.
Uniqueness of solutions
Activity 4: Complete the Sudoku puzzle on the right as much as possible. What (surprising?) fact do you observe?
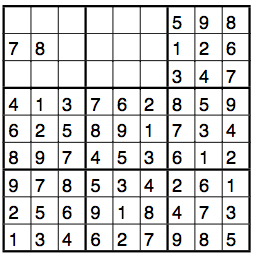
Activity 5: Assume you are given a 9x9 Sudoku in only 3 cells are empty, and all other cells were filled in correctly. Also assume that the puzzle has at least one solution. Explain why there can be at most one solution.
In activity 4, we learned that a 9x9 Sudoku with only four empty cells still need not have a unique solution. On the other hand, we show in activity 5 that every solvable 9x9 Sudoku with no more than 3 empty cells has at most one solution.
Here is one more interesting conjecture: the smallest number of of filled-in cells that is needed for a 9x9 puzzle with a unique solution is probably 17 (http://en.wikipedia.org/wiki/Mathematics_of_Sudoku#Ordinary_Sudoku). Several puzzles have been found that need only 17 filled-in cells for a unique solution, and it is very unlikely (based on an extensive search using computers) that puzzles which have a unique solutions with only 16 clues or less exist.
Aside from those results, there are no easy-to-use criteria to decide whether a Sudoku has a unique solution or not. However, Sudoku puzzles in newspapers or books usually contain puzzles with unique solutions only.
Existence of solutions
Given a Sudoku puzzle, can we decide in a systematic way if there is at least one way of filling it in? Yes, we can. However, in many cases it’s quite a lot of work. We will learn about a suitable method in one of the later sections.