Activity 1: This is almost completely solved in the 2 paragraphs below the activity.

Activity 2: The 12 easy places are: the last cell to be filled in each 3x3 box with a thick margin (unless they happen to be at the end of a row, in which case we already observed that there is at most one possibility), as well as the last cell to be filled in each column (unless they happen to be at the end of a row, or the last cell to be filled in a 3x3 bow, in which case we already observed that there is at most one possibility). As a result, the numbers N1 to N12 are 7,4,7,4,9,8,7,6,5,4,3,2. Their product is (9x8x73x6x5x43x3x2), and our earlier estimate for the number of complete Sudoku puzzles was thus too big by a factor of at least (9x8x73x6x5x43x3x2). Thus a better estimate is (9x8x7x6x5x4x3x2x1)9 / (9x8x73x6x5x43x3x2)=3.8x1041 .

Activity 3: The red cell can contain no numbers other than 1 and 3, since all other numbers appear in the same row or box. However, in the “Clever counting” section, we estimated that there were no more than 4 ways of filling the cell in. Therefore, our estimate is too big by at least a factor of 2.

Activity 4: Having completed the puzzle as much as possible, there should now only be 4 empty cells, with the puzzle looking as follows:

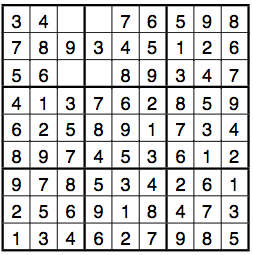
It is interesting to note that although only four entries are missing, the solution of the puzzle is still not unique.

Activity 5: If a puzzle has just 3 empty cells, then at least one of them must be alone in its row or column (make sure you understand why). Since the puzzle has a solution by assumption, there is a way of filling this cell in. Moreover, there is only one way of filling it in, since this cell is the only empty one its row or column. Fill it in. There are now just two empty cells in the entire puzzle. They are both either the only empty ones in their row or the only empty ones in their column. Now an argument like the one for the first of the three empty cells shows that there is a unique way of filling the two cells in.

Activity 6: You’re on your own, since I can’t provide solutions for a multitude of programming languages.

Activity 7: The algorithm tries to fill the puzzle cell by cell, trying all possible numbers until all possibilities have been exhausted or until a solution has been found. Therefore, if there is a solution, the algorithm will find it. To make the algorithm find all solutions, simply don’t stop once you have found the first one! More specifically, once you are in step 4a of the algorithm and are at the last cell in the enumeration, copy down the solution. Then erase the number you entered in the last cell of the enumeration, then make the second-to-last cell of the enumeration the new current cell, and continue with step 3 of the algorithm.

Activity 8: The main point of the activity is to observe that hard Sudokus can usually not be solved by switching back and forth between candidate-checking and place-finding.

Activity 9: Let’s assume without loss of generality that the preemptive set under discussion lies completely in row 1. Then the solution will have the number x in one of the cells belonging to the preemptive set. But each number may only occur once per row, so the solution cannot contain the number x in those cells of the first row that do not belong to the preemptive set.

Activity 10: This one is indeed super tough. I will not point out all the time which step of the algorithm I am at, but you should try to keep track of this yourself, to make sure that you understand that there is a method to this. First use the place-finding and candidate-checking methods to fill in as much as you can, then mark up the puzzle. I did not find any preemptive sets, but there were several cells whose markups only contained two numbers. I chose c(6,1), which had a markup of 1 and 9, and entered a 1. This immediately allowed me to cross out  the number 1 in the markups of a large number of cells, and the candidate-checking and place-finding methods allowed me to fill in several more cells. Once I could not make any more progress, I chose cell c(3,9), which had a markup of 3 and 7, and entered a 3. The place-finding and candidate-checking methods as well as the method of preemptive sets then lead to the following solution:

Activity 11: The first part of the activity is easy and will not be solved here.

A directed graph is a graph whose edges have a direction associated with them, usually indicated by arrows on the edges. One could for example think of the cardiovascular system, which is composed of arteries and veins through which blood flows, and points where two blood vessels meet. The arteries and veins correspond to edges, and the meeting points of blood vessels correspond to vertices. Since blood flows in only one direction through an artery or vein, we can associate a direction with each edge.

A weighted graph is a graph where each edge has a number (‘weight’) associated with it. For example, if you represent a network of roads as a graph, the weights could stand for the lengths of roads.

Activity 12: The Chinese postman problem is about how to find the shortest path through a graph that goes through every edge at least once and ends up at the starting point. A postman might be interested in the answer to such a question, since he wants his path to be as short as possible, needs to visit every street at least once, and needs to finish his route where it began.

The shortest path problem is about finding the shortest route between two points on a graph. Routing applications need to solve problems like this all the time when they find the shortest route from one town to the other.

The traveling salesman problem is about finding the shortest path through a graph that visits every vertex at least once, and starts and ends at the same point. Imagine a salesman who needs to visit all of his clients, and wants to drive as short a distance as possible.

The max-flow min-cut theorem is about flows on a weighted graph: imagine you have a network of pipes, and each of them has a certain maximal capacity. You want to pump a fluid through the network from one point to a different point. The max-flow min-cut theorem helps you work out how the fluids should flow through the network to get the greatest possible throughput.