Mathematics and Sudokus: Solving Algorithms (II)
Crook’s pencil-and-paper algorithm
You probably noticed in the previous activity that there are indeed Sudokus that cannot be solved using method 2 or 3. James Crook, professor emiritus of Computer Science at Winthrop University, came up with an algorithm that will solve any Sudoku puzzle, and can be done on paper. The following discussion is in part adapted from his paper “A Pencil-and-Paper Algortihm for Solving Sudoku Puzzles”, which is available at http://www.ams.org/notices/200904/rtx090400460p.pdf.
Crook uses a hybrid approach, which is a sophistated combination of our simple solving algorithm, the place-finding method, the candidate-checking method, and the method of preemptive sets, which we will learn about in a minute. Remember that the candidate-checking and place-finding methods are nice and fast, but sometimes fail. Our simple solving algorithm can solve everything, but is not very easy to do for humans, because there are so many combinations to check. Crook’s method of preemptive sets reduces the number of combinations in a clever way.
Definition: The mark-up of a cell is a list of numbers that the cell may contain, given the numbers that are already in the cells of its row, column and box.
Mark-ups will help be an important tool in our algorithm. We will often write the mark-up in small print in the bottom right corner of a cell.
Let’s think again about the simple solving algorithm worked: for each cell, we entered numbers between 1 and 9 into cells cell by cell. If we found that our choices violated the Sudoku condition, we erased one or more numbers, entered new numbers and tried again. As a result, there were many situations where we tried a lot of numbers which all lead to violations, before finding the correct one. In an improved version of the simple solving algorithm, one could first mark up the puzzle, and then for each cell not try numbers 1 to 9 in increasing order, but only the numbers from the markup: this means that there are fewer checks to do, thus less work. Here is another modification: first use the candidate-checking and place-finding methods on the puzzle, then mark it up, and finally use the simple solving algorithm to deal with whatever could not be solved using the other methods. This is, in part, what Crook’s algorithm does.
Definition: A preemptive set is a list of m numbers, 2 ≤ m ≤ 8, each of them between 1 and 9, together with a list of m cells, with the property that no numbers other than the m numbers from the list can occupy the m cells.
To refer to cells, Crook uses a notation where for example c(2,1) refers to the cell in row 2 from the top, column 1 from the left. He denotes preemptive sets by first listing the numbers belonging to it, and then the cells that they might occupy: For example, {[4,7], [c(2,1),c(2,9)]} refers to the preemptive set consisting of the numbers 4 and 7 lie in the cells c(2,1) and c(2,9).
Here is an easy-to-prove but extremely useful theorem about preemptive sets:
Theorem (Occupancy theorem): Suppose that x is a number that appears in a preemptive set, which lies completely in one column (or row, or 3x3 box). Then there can be no occurence of x in that column (or row, or 3x3 box) outside of the preemptive set.

Activity 9: Explain in a paragraph why the Occupancy theorem is true.
Suppose that we are solving a Sudoku puzzle and have discovered a preemptive set. If the preemptive set lies completely within one column (or row, or 3x3 box), then the occupancy theorem allows us to cross out any numbers that appear in the preemptive set from the markups of cells outside of preemptive sets in that column (or row, or 3x3 box). We now have three methods of working towards solutions of Sudoku puzzles that work well on paper: methods 1 and 2, and the method of preemptive sets, which helps allows us to cross numbers out in the markups of cells.
We can now state Crook’s algorithm for solving Sudoku puzzles on paper:
1.Use methods 2 and 3 alternatingly to complete the puzzle as much as you can, until those methods lead no further.
2.Mark up all empty cells of the puzzle.
3.Look at each column, row and 3x3 box and try to break it down into preemptive sets. Try to break preemptive sets with several elements down into smaller preemptive sets. Whenever you have found a preemptive set, cross out numbers in the markups of cells whenever the Occupancy theorem allows it. Try to use methods 2 and 3 again if you were able to cross out numbers from the markups of any cells. Repeat this process until you can find no more preemptive sets, or until the Sudoku rule is violated.
4.There are now several possibilities:
a. If you have solved the Sudoku puzzle,then you are done.
b. If you violated the Sudoku condition, then the Sudoku does not have any solutions and you are done.
c. If neither is the case, then proceed to step 5.5.Choose an empty cell, call it the "current cell" and enter a number from its markup. Assign the current cell a colored pen that you have not used before. Note the current cell, the number you entered and the color of the pen on a separate sheet of paper.
6.Look at each column, row and 3x3 box and try to break it down into preemptive sets. Try to break preemptive sets with several elements down into smaller preemptive sets. Whenever you have found a preemptive set, cross out numbers in the markups of cells whenever the occupancy theorem allows it. Try to use methods 2 and 3 again if you were able to cross out numbers from the markups of any cells. Whenever you enter a number, use the current color, i.e. the pen chosen in step 5. Repeat this process until you can find no more preemptive sets, or until the Sudoku rule is violated or there is a cell whose markup is empty (contains no numbers).
7.There are now several possibilities:
a. If you have solved the Sudoku puzzle, then you are done.
b. If there is a cell whose markup is empty, then the choice that you made in step 5 does not lead to a solution. Erase everything that you have entered using the current color, and moreover erase the number you entered in step 5 from the markup of the respective cell. The the markup if this cell is now not empty, go to step 5. Otherwise, repeat the erasing for the previous color (remember that you have a list of cells with their corresponding colors and entries): erase all entries made using the color, and also erase the number entered in the corresponding cell. Repeat until you end up with a non-empty markup. If this state is not reached, then the puzzle does not have a solution and you are done. If you do reach the state, go to step 5.
c. If none of the previous cases applies, go to step 5.
Crook’s algorithm in an example
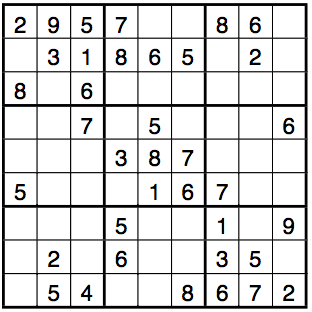
To illustrate the algorithm, we will solve the below (difficult) Sudoku, which Crook discusses in his paper. The puzzle itself is from the book “Solving Sudoku” by Michael Mepham (see References).
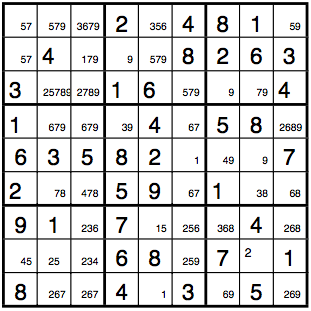
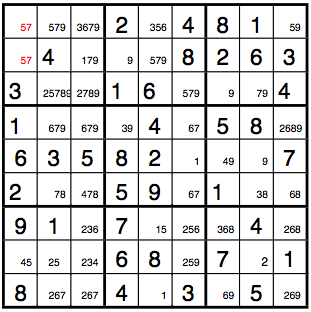
After steps 1 and 2 of the algorithm, the Sudoku board looks as follows:
In part 3 of the algorithm, we immediately find the preemptive set {[4,7], [c(2,1),c(2,9)]}. By the occupancy theorem, we may eliminate 4 and from the markups of all cells in the top-right 3x3 box. This exposes the 9 as the only candidate for cell c(2,7), so we enter the 9.
Continuing to look for preemptive sets, we find the preemptive set {[2,4,9],[c(4,4),c(4,6),c(4,7)]}, and after removing the respective numbers from the markups in row 4, we find the preemptive set {[1,3,8],[c(4,1),c(4,2),c(4,8)]}.
Looking over the board one more time, we see that there are no other preemptive sets, and that methods 2 and 3 would not allow us to enter any further numbers into cells either. We thus move on to step 5 of the algorithm.
At this point, it is a good idea to copy the entire Sudoku board with the markup and continue working on a separate sheet of paper. When choosing a cell to enter a number from its markup, it is usually best to choose a cell with a markup consisting of as few numbers as possible (why, and what is the exception to this rule?). In our case there are several cells with a markup consisting of 2 numbered. For instance, we could enter a 7 into c(2,1) using a red pen.
In step 6 of the algorithm, we use methods 2 and 3 to enter the numbers 7,4,4,8 and 8 into the cells c(2,1, c(3,2), c(2,9), c(6,2), and c(7,9) respectively. At this point we get a violation of the Sudoku condition, since the middle 3x3 box on the right cannot contain the number 8. As a result, we erase everything we worked out in red, erase 7 from the markup of c(2,1) and proceed to step 5. (In practice, it is probably easier to copy the state of the puzzle before we started using red onto a new sheet of paper.)
In step 5, we observe that the markup of cell c(2,1) now only contains one number, so we choose this cell and enter 4. In step 6, we write 7 into cells c(3,2) and c(2,9). We are now unable to find any further preemptive sets or make progress with methods 2 or 3, so we go back to step 5.
This time, we choose cell c(9,8) and enter the number 4 from its markup in green color. This time we are lucky: the use of methods 2 and 3, as well as the method of preemptive pairs, will solve the puzzle for us in step 6 of the algorithm. One way of completing the puzzle is as follows:
cell entry
c(7,8) 8
c(8,9) 4
c(8,3) 8
c(6,9) 8
c(4,2) 4
c(2,9) 7
c(2,1) 4
c(3,2) 7
c(7,2) 6
c(7,3) 3
c(7,1) 7
c(8,5) 7
c(9,5) 3
c(6,2) 4
c(5,2) 1
c(5,1) 6
c(4,1) 3 (using the preemptive pair {[1,3],[c(1,9),c(3,9)]})
c(6,8) 3
c(1,5) 4
c(7,9) 5
c(3,8) 4
c(3,7) 5
c(5,8) 9
c(4,8) 1
c(5,7) 4
c(5,3) 2
c(4,7) 2
c(6,4) 2
c(7,6) 4
c(4,6) 9
c(4,4) 4
c(7,5) 2
c(3,5) 9
c(3,4) 1
c(1,6) 3
c(3,6) 2
c(1,9) 1
c(3,9) 3
c(8,6) 1
c(9,4) 9
c(9,1) 1
c(8,1) 9
We have thus found the following solution for the puzzle:
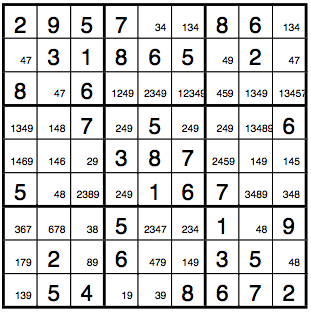
Activity 10: Use Crooks algorithm to solve the Sudoku puzzle below. It was published by www.krazydad.com at http://www.krazydad.com/sudoku/sfiles/KD_Sudoku_ST_8_v1.pdf and is the first puzzle in a krazydad’s first book of super tough puzzles. You will likely spend several hours on this it. The puzzle has a unique solution. After some trying, I was able to solve the puzzle by guessing (the correct) numbers for just two cells in step 5 of Crook’s algorithm, but there might be even faster ways of solving the puzzle.
