Abstract: Many of the classical functors $F:\mathcal{C}\to\mathcal{D}$ of homological algebra and algebraic topology factor through a ``definable version'' of the category $\mathcal{D}$, as in the following diagram: 

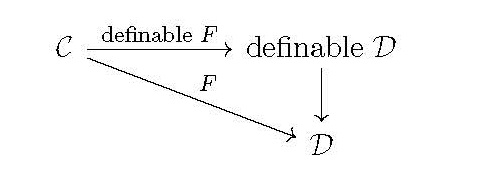
The corresponding ``definable $F$'' provides significantly stronger invariants for the spaces or groups in $\mathcal{C}$, particularly when the latter are limit objects such as the solenoid (pictured). As examples, we describe definable Ext and $\mathrm{lim}^1$ and \v{C}ech cohomology functors, showing that each distinguishes among uncountable classes of objects whose corresponding classical invariants are constant. As the terminology ``definable'' might suggest, this work represents an infusion of descriptive set theoretic techniques into algebraic contexts; it is joint with Martino Lupini and Aristotelis Panagiotopoulos.