Background
We will motivate our studies of Orthogonal Polynomials on the Sierpinski Gasket. In this page we will discuss classical Orthogonal Polynomial Theory on the unit interval. Then See the links below for further information.
- Monomials on SG: We will dicuss the construction of monomials on the Sierpinski Gasket as done in the paper by Needleman et. al.
- Recurrence Relation: We will describe the recurrence relation for constructing OP on the Sierpinski Gasket
- SUMS Poster: the poster presented at the SUMS Conference, summary of findings
Motivation: Classical Orthogonal Polynomial Theory
Previous REU students developed monomials for the Sieprinski Gasket. These monomials are analogs to the polynomials xn/n! on the unit interval.
The goal of this project was to orthogonalize these monomials to produce analogs to the Legendre Polynomials on the unit interval.
Orthogonal Polynomials πk(x) on the unit interval can be contructed by using the Gram-Schmidt process with an inner product such as:
<π k(x),π j(x)>= ∫01 πk(x) πj(x) w(x) dx
where w(x) is a weight function on [0,1]. The Legendre polynomials have weight w(x) = 1.
However, the Orthogonal Polynomials also obey a three term recurrence relation:
πk+1(x) = (x − αk) πk(x) − βk πk-1(x)
This recurrence relation makes computation of the OP fast, and is used in many applications such as interpolation. We want to construct OP in the Sierpinski Gasket in order to make these numerical methods available.
Other properties of classical OP is that as the degree increases, so do the number of zeros. In addition, the zeros "interweave". That is a zero on the k-th OP lies between two zeros on the (k-1)-th OP.
We also are interested in the dynamics of orthogonal polynomials. Below is an example for
the Legendre polynomials. Fix a point x in the unit interval I. Then we want to plot
( πk(x), πk+1(x) ) ,
where πk+1(x) is the k-th degree orthogonal polynomial.
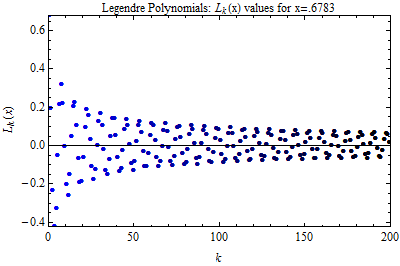
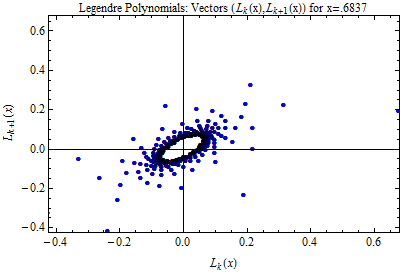
In general, the dynamics are drawn to an attractor. In the Legendre case, this attractor is a circle. In general it should be some Julia set (why?) What are the dynamics of the OP in the Sierpinski Gasket?
For dynamics of orthogonal polynomials on the unit interval for fractal measures, see Orthogonal polynomials with respect to self-similar measures - S. Heilman, P. Owrutsky, and R. Strichartz
