Monomials
Definitions of Derivatives
The Sierpinski Gasket can be seen as the limit of a sequence of graphs Γm. We can define the graph Laplacian on SG as the renomalized limit of graph Laplacians on each level:
Δ u(x) = limm → ∞ (3/2) 5m Σ{x∼y} (u(y) - u(x))
There are two derivatives on SG: the normal derivative and tangenetial derivative
∂n u(qi) = limm → ∞ (5/3)m (2u(qi) -u(Fmi qi+1) -u(Fmi qi-1))
∂T u(qi) = limm → ∞ 5m (u(Fm0 qi+1) - u(Fm0 qi-1))
Definitions of the Monomials
The monomials are the kernels of the operator Δj. We let Hj be the space of functions f satistying Δjf =0. Hj is also called the set of polynomials of degree less than or equal to j.
For i=1,2,3 and j≥0, the monomials Pji are defined to be the functions in Hj satisfying:
- ΔmPji(q0) = δm,j δi,1
- ∂nΔmPji(q0) = δm,jδi,2
- ∂TΔmPji(q0) = δm,jδi,3
The set of monomials {Pki | i = 1, 2, 3; and k = 0,…, j} is a basis for Hj.
Moreover, the monomials satisfy ΔPji = P(j-1)i.
Graphs of Monomials
Below we plot some of the graphs of the monomials. Note that Pj1 and Pj2 are both symmetric with respect to the axis bisecting the angle at q0. Likewise, Pj3 is antisymmetric with respect to the same axis.

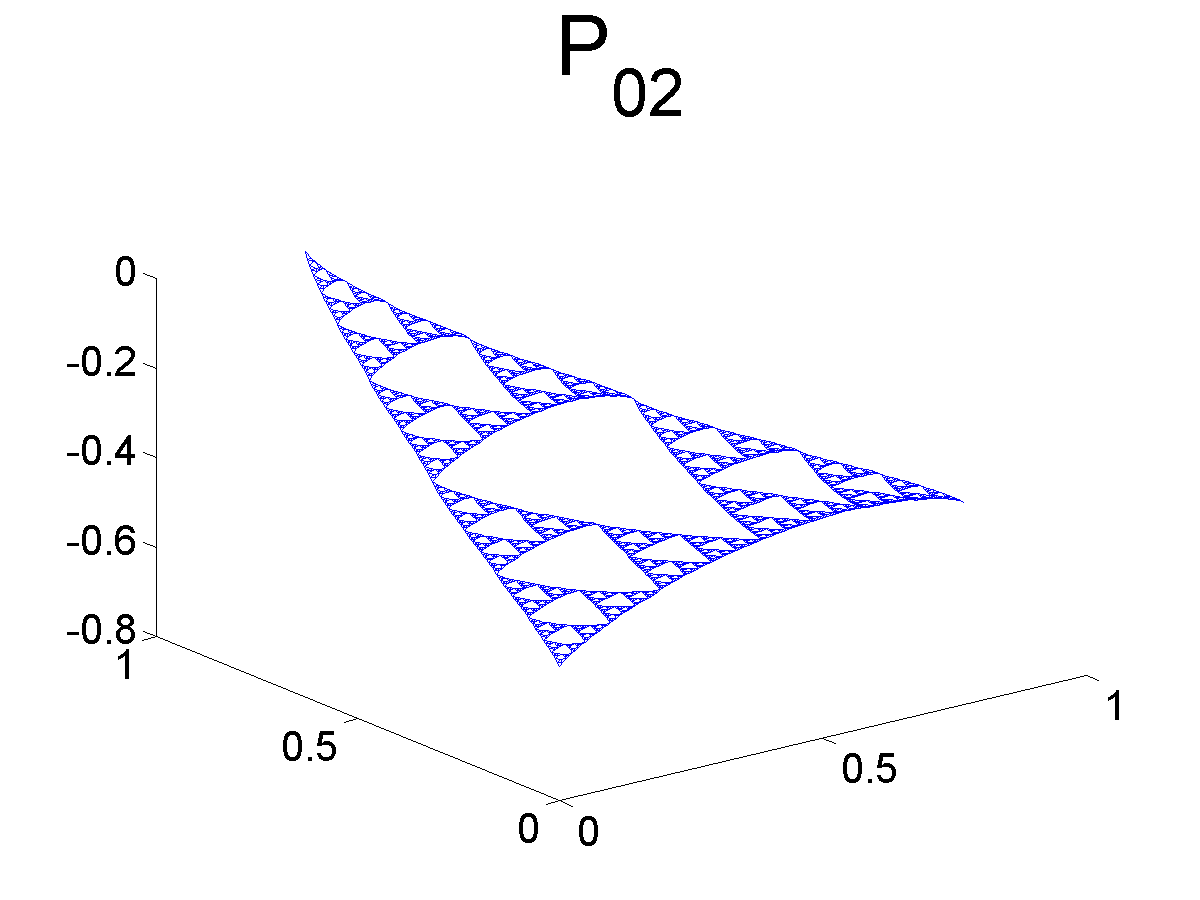
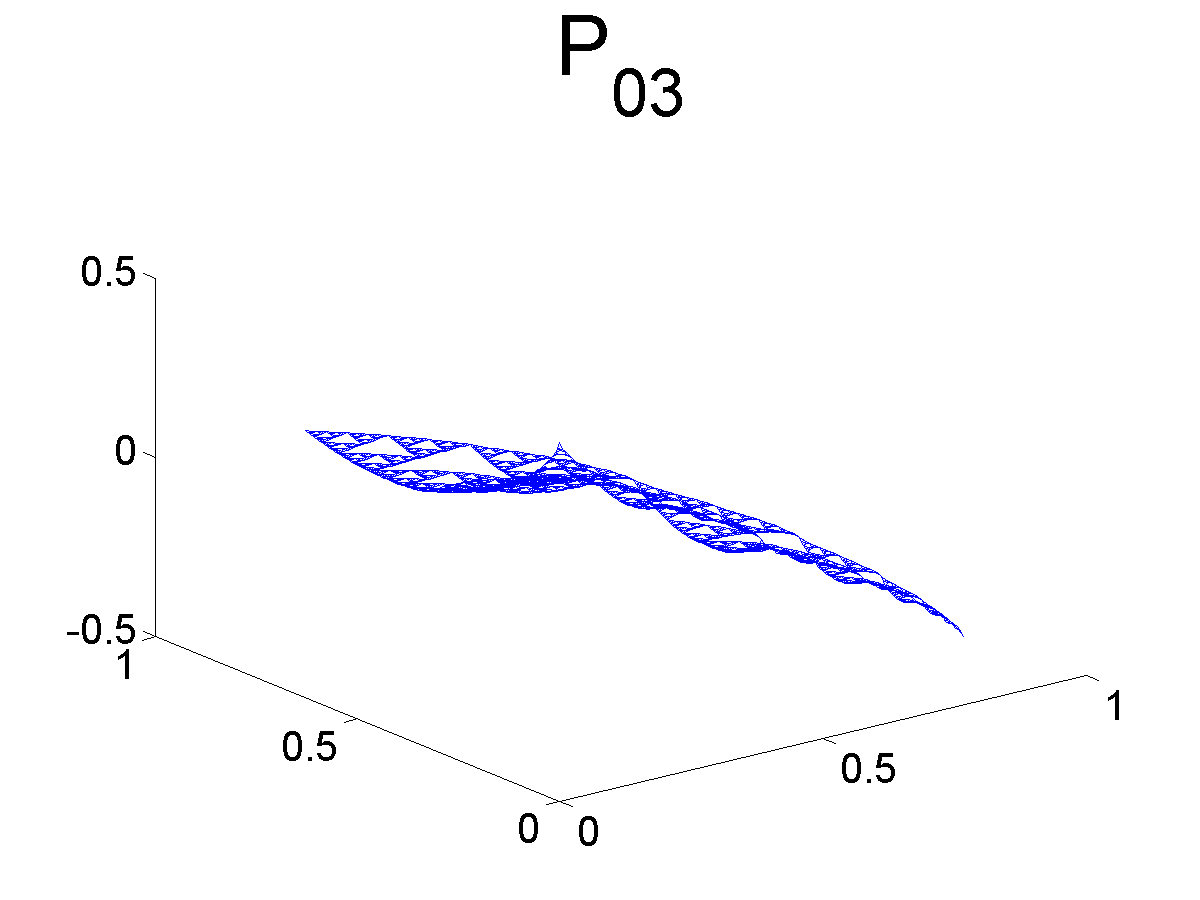
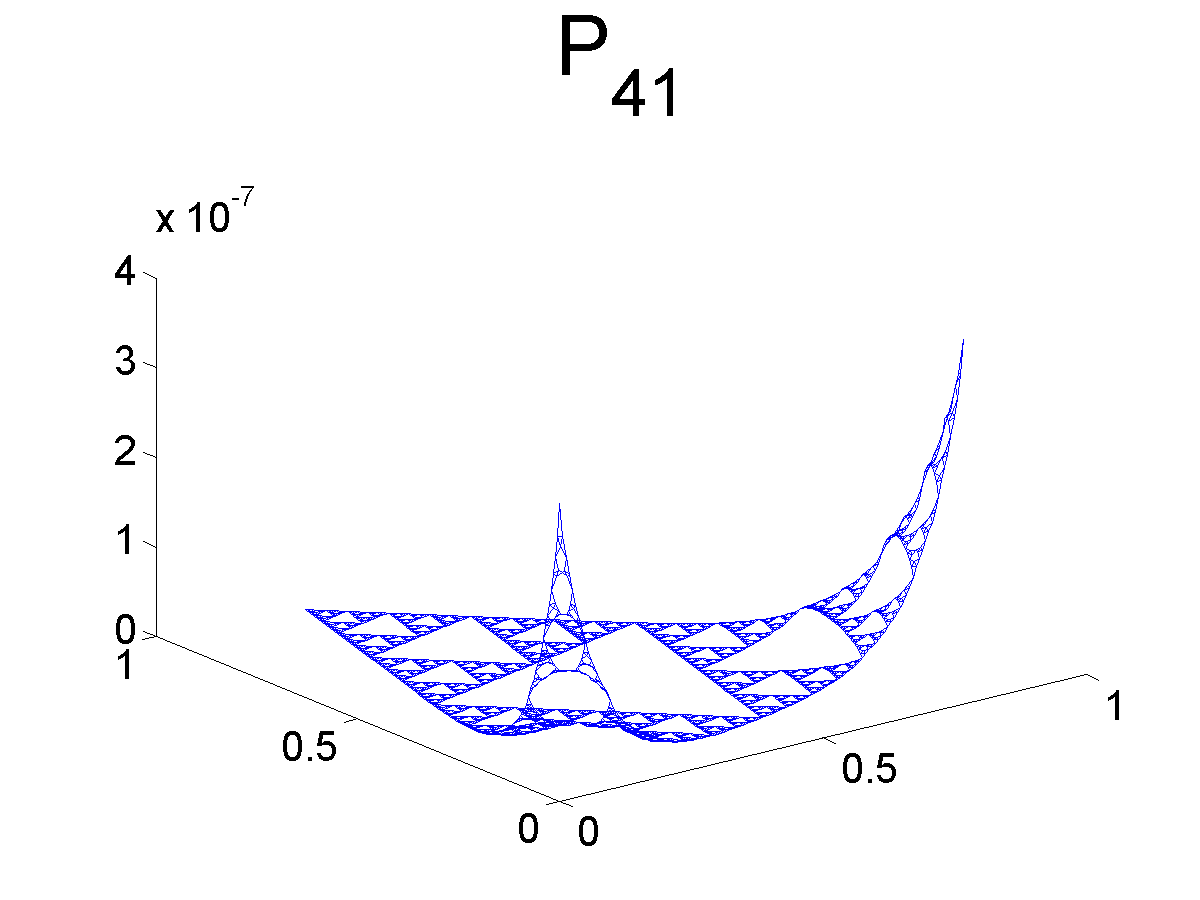
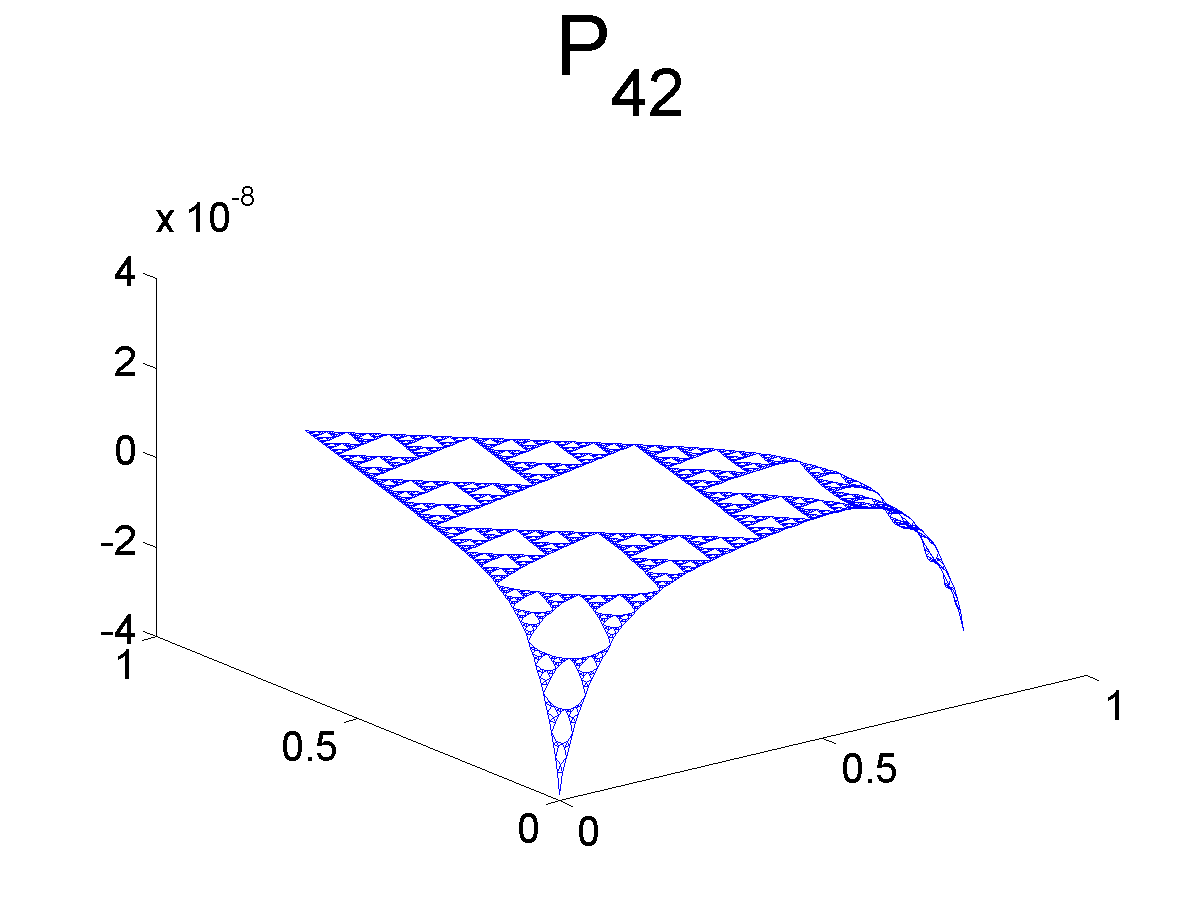
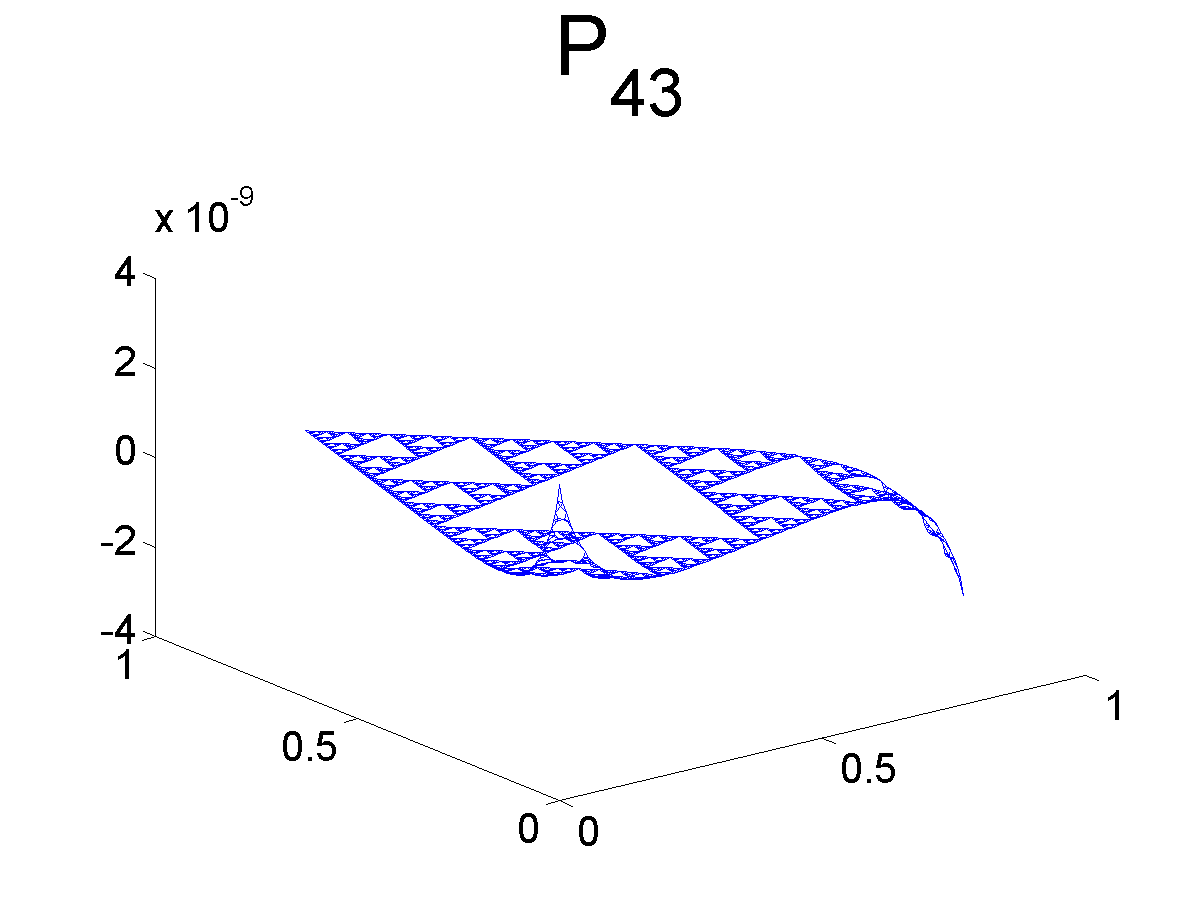
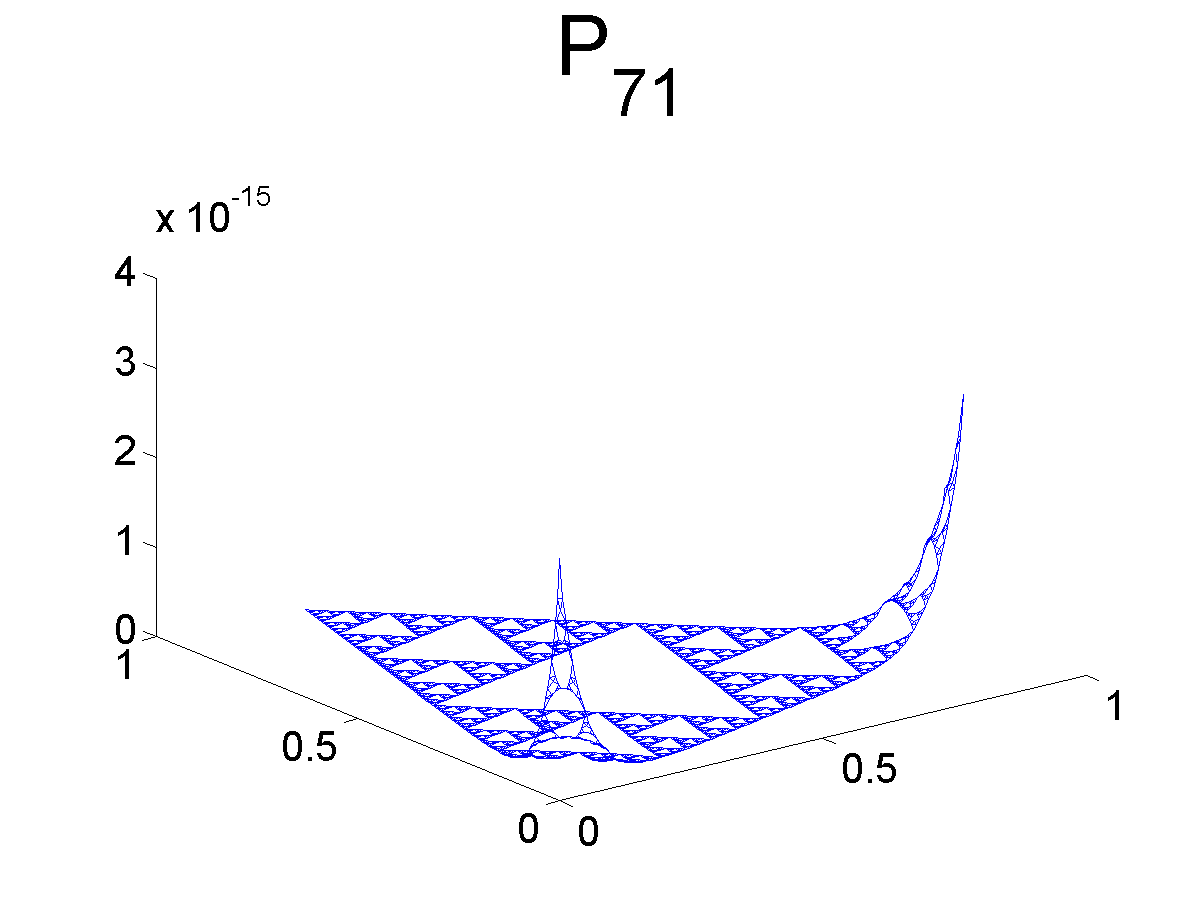
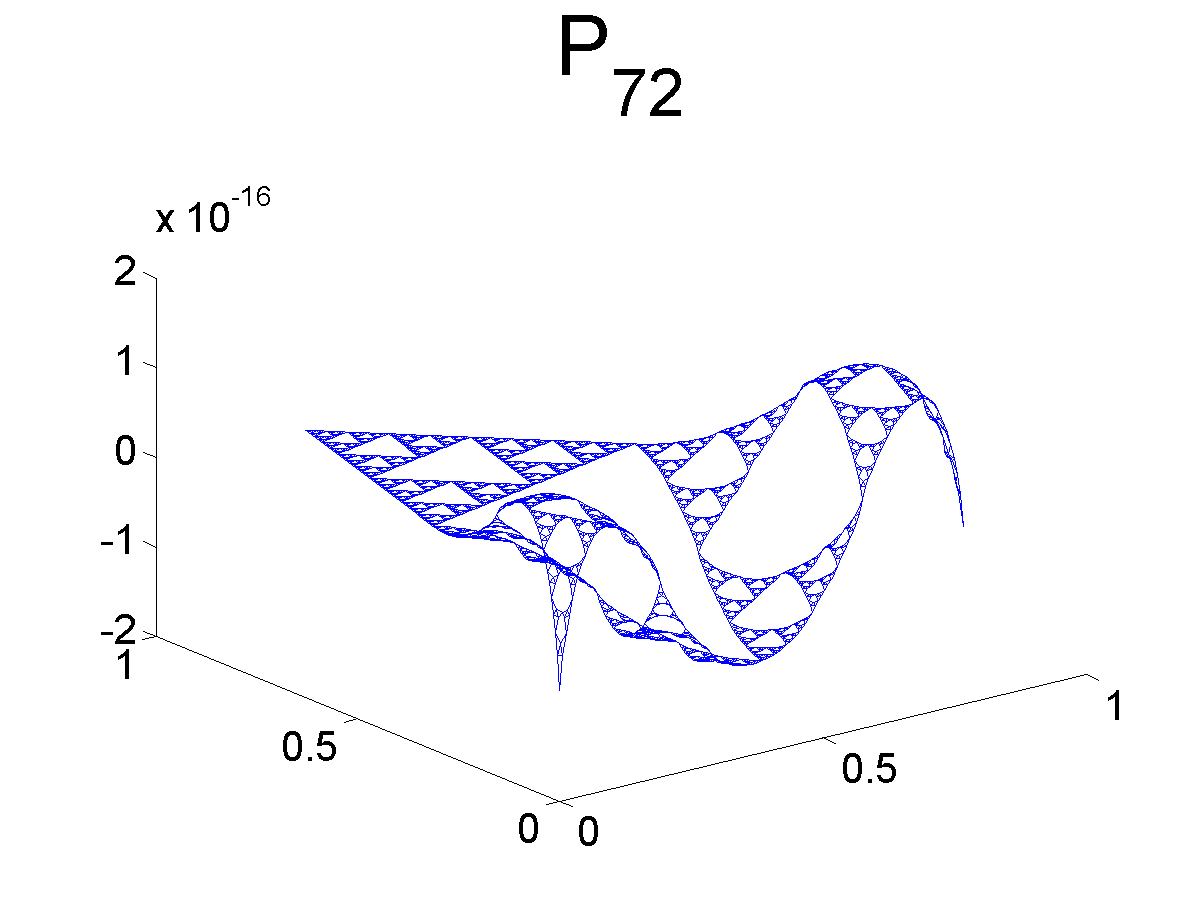
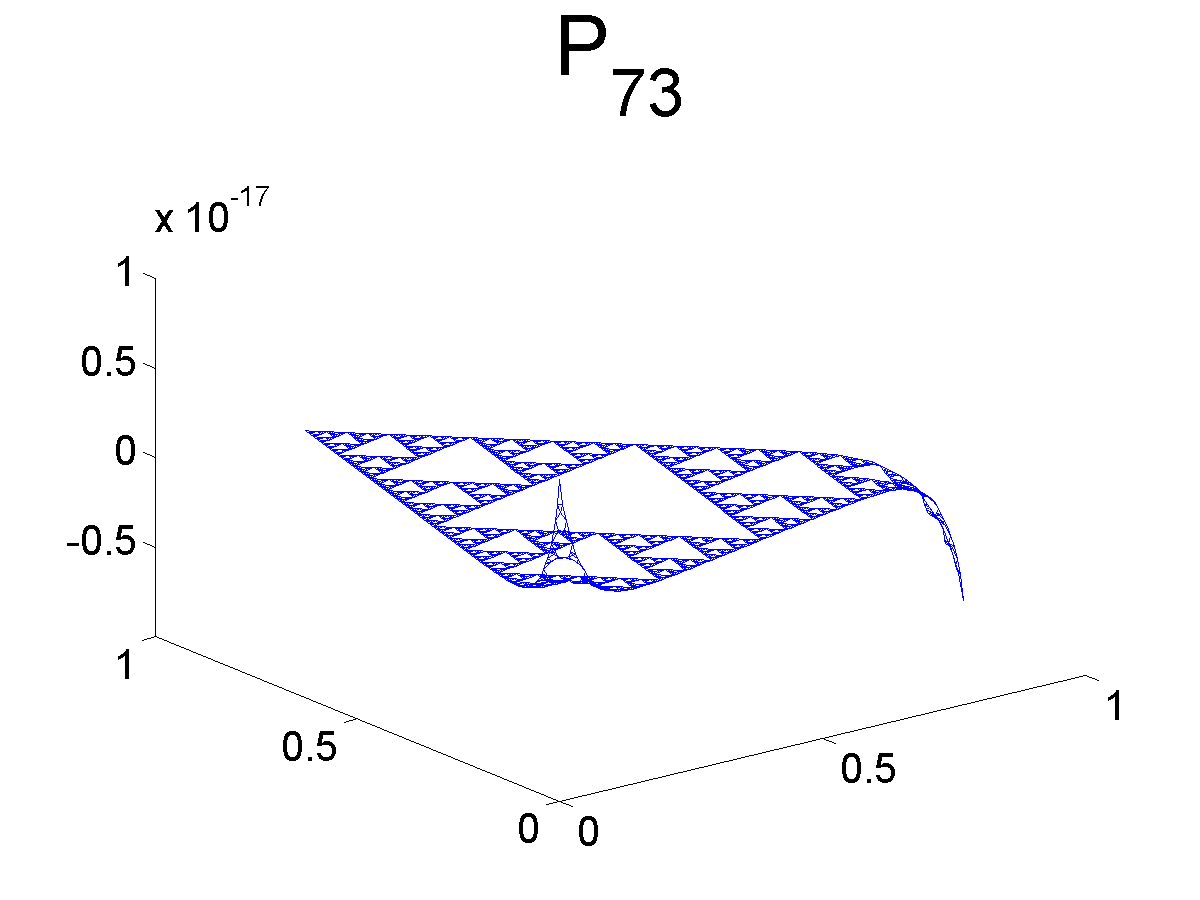
Further Information
For the complete theory of the monomials on the Sierpinski Gasket, see the paper "Calculus on the Sierpinski gasket I: polynomials, exponentials and power series by Needleman, Strichartz, Teplyaev, and Yung. As well, visit their website at Polynomials and Power Series on SG.
