Determinism and Chaos

Chaos theory is the study of how systems that follow simple, straightforward, deterministic laws can exhibit very complicated and seemingly random long term behavior. A classic example of this is the weather. Individual molecules of air all conform to basic laws of physics, but global weather patterns are anything but simple.

A hallmark of chaotic systems is sensitive dependence on initial conditions. This means that if two copies of the system differ by only a very small amount, then after a relatively short period of time, the two systems will diverge and appear very different from each other. The "butterfly effect" is an example of this, alluding to the idea that the flap of a butterfly's wings in Africa can cause a cascade of events culminating in a tornado in Texas. This sensitive dependence on initial conditions also guarantees that weather forecasting will not be accurate for more than a few days in advance.

Chaos can also be seen in systems as diverse as electrical circuits, oscillating chemical reactions, and fluid dynamics, and planetary bodies orbiting each other. However, many real world systems such as the weather involve far too many particles to analyze precisely with computers, but much of the essential behavior which makes these systems chaotic can also be found in much simpler systems that are much more easily analyzed with pencil and paper and simulated with computers. Researchers study these simpler systems in the hope that they will shed light on the more complicated real-world phenomena.

Lorenz's Waterwheeel

In the 1960s, Edward Lorenz, a meteorologist experimented with primitive computer simulations of. His program used twelve recursive equations to simulate rudimentary aspects of weather; he entered several variables into his program each time he ran it, and watched to see what types of weather patterns such initial conditions would generate. He could print out graphs of fluctuating temperatures or other conditions.

One day, Lorenz tried to recreate an interesting weather pattern, one he had seen previously, by re-entering the values the computer had previously calculated and reported. However, when he ran the program again, his results were different from the initial run. Lorenz suspected a bug, but after checking the two plots, however, he realized his "error": on his previous computer printout, the one he had used to enter the initial conditions into the computer for the second trial run, the figures were printed with three significant digits. In the program, all values were calculated to six significant digits. Lorenz had assumed that the difference, only one part in a thousand, would be inconsequential. However, due to the recursive nature of the equations, little errors would first cause tiny errors, which would then affect the resulting next calculation a bit more, which would affect the output of the next run even more. The final result of a long string of recursive calculations would lead to a weather pattern totally different from the expected values.

A further simplification of Lorenzs' already oversimplified model can actually be constructed. Imagine a waterwheel with eight buckets spaced equally around its rim. The buckets are mounted on swivels, much like Ferris-wheel seats, so that the buckets will always open upwards. At the bottom of each bucket is a small hole. The entire waterwheel system is then mounted under a waterspout.

Begin the flow of water from the waterspout. At low speeds, the water will trickle into the top bucket, and immediately trickle out through the hole in the bottom. Nothing happens. Real boring. Increase the flow just a bit, however, and the waterwheel will begin to revolve as the buckets fill up faster than they can empty. The heavier buckets containing more water let water out as they descend, and when the water is gone, the now-light buckets ascend on the other side, ultimately to be refilled. The system is in a steady state; the wheel will, like a waterwheel mounted on a stream and hooked to a grindstone, continue to spin at a fairly constant rate.

But even this simple exhibits chaotic motion. Increase the flow of water, and strange things will happen. The waterwheel will revolve in one direction as before, and then suddenly jerk about and revolve in the other direction. The conditions of the buckets filling and emptying will no longer be so synchronous as to facilitate just simple rotation; chaos has taken over.

A real-life implementation of a Lorenz waterwheel by Gordon McDonough:

The waterwheel is supposed to represent a grossly oversimplified model of how air in a column rotates. Contact with the ground heats air, and it rises. The air higher up in the atmosphere slowly cools and is made denser and falls. These two bodies of air have to get around each other, and by slipping by each other, they induce a rotation. The waterwheel is an inverted model of this process. The water in each bucket signifies the heat in that pocket of air. The bucket picks up water when the air is close to the ground (the top of the wheel), and all of the buckets are constantly, but slowly, losing water, which corresponds to air losing heat through radiation. The hotter the air is, the more forcefully it's pushed upwards, which corresponds to buckets with more water being pulled down more strongly.

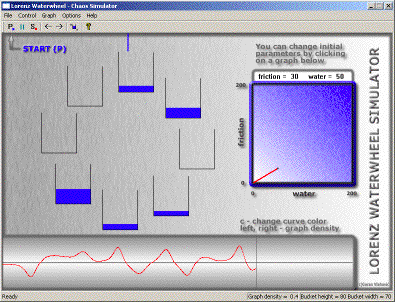
A computer simulation of the Lorenz Waterwheel written by Goran Vlahovic

Screenshot of Goran Vlahovic's program:

There is also a java applet created by Fritz Gassmann simulating a waterwheel which can be found at here.

Behavior

There are four distinct kinds of behavior that the waterwheel can exhibit:

• It can stop rotating
• It can rotate constantly in one direction
• It can rotate periodically back and forth
• It can rotate chaotically with no easily recognized pattern or repetition