Before we move on to the definition of a group and spend some time working through examples, we will spend some time introducing some fundamental concepts about sets and operations. These two notions are indeed at the heart of the definition of a group, as well as that of many other algebraic constructions. Sets pertain to set theory, while sets with operations and maps make us enter the realm of algebra. The following presentation should make it straightforward to study those constructions.

A Little Set Theory

The ideas of set theory and their algebra are deeply fundamental concepts on which all areas of mathematics rely. Even the algebra of real numbers, that you probably use every day, is based on those ideas. Nevertheless, this topic is often neglected and many science students go through college without ever having a good grasp of it and never realize the big paradoxes that carelessness with set theory can lead to.
This short introduction, while not a complete study of set theory, should at lest get a little more comfortable with and aware of the common paradoxes threatening you. We borrow the first paragraph from this document by Matthew Slatzman. The approach in the rest of this text is different and original, though.

What is a Set? A set is one of those fundamental mathematical ideas whose nature we understand without direct reference to other mathematical ideas. Quite simply, a set is a collection of distinct objects. The objects can be real, physical things, or abstract, mathematical things. The number of such objects can be finite or infinite. The only important thing is that the objects be distinct, i.e., uniquely identifiable. This idea of distinctness has some subtleties. For example, a collection of identical blue balls in an urn (you meet a lot of these in probability class) is a set because the balls are in principle uniquely identifiable: we could paint a different number on each of them. On the other hand, the list of digits 1, 5, 3, 2, 1, 4 is not a set, because there is no way to distinguish the two occurrences of 1 in the list. (Order doesn't matter when listing the elements of a set.)

In set theory, the proper way to define a set is to provide a rule to determine whether any given object belongs to that set, and there are two basic ways to do so:

• (D1) The most basic way is to list all the elements in the set between curly braces. For example, the expression {2, 4, 6, 8, 10} defines the set that contains the elements 2, 4, 6, 8 and 10. If the given element does not appear in the list, it does to belong in the set.
• (D2) The other way is to define sets as subsets of already defined sets. If X is an already defined set and P is a property that elemets in X may or may not have (we say of elements that have it that they satisfy P) , the expression { x ∈ X : x satisfies P} defines a set whose elements are all those elements of X that satisfy P. The ":" is read "such that" (Some authors use "|" instead.), and to check whether a given element is in the set, on simply checks that the elements belongs to X (which was already defined when we defined X itself) and then checks that it satisfies P.
  For example, assuming the set N of natural numbers was already definied, one can use the following notation {x ∈ N : x is divisible by 17} to denote all the natural numbers that are multiples of 17.

If an element x belongs to a set X, we say that it is an element of X. We write x ∈ X and read it "x is in X". Also, a special notation is reserved for the empty set: no element belongs to it. We write ∅ for the empty set.

On top of these two fundamental ones, there are other ways of defining a set. For example, given two already defined sets S and T, on can define:

• The union S ∪ T of S and T: an element x belongs to S ∪ T if an only if it belongs to at least one of either S or T.
• The intersection S ∩ T of S and T: an element x belongs to S ∩ T if an only if it belongs to both S and T at the same time.
• The cartesian product S x T: elements of are ordered pairs (s, t) where s is an element of S and t is an element of T.

For example, if S = {a, b} and T = {b, c}, then S ∪ T = {a, b, c}, S ∩ T = {b} and S x T = { (a,b) , (a,c), (b,b), (b,c) }.

Why be careful? The most sensitive definition amongs those given here is (D2) without any doubt. In particular, it is crutial that the new set be defined as a subset of an existing one. Giving the property alone is not enough and forgetting that leads to some of the most famous paradoxes in set theory and mathematics.

One of the problems with early definitions of set theory was to allow expressions as "the set of all sets". Following our definition, this is not a valid set because we neither listed all of its elements between brackets, nor did we define it as a subset of an already defined subset. Nevertheless, if one tries to think of that as a set, one can ask whether it belongs to itself -- it is nothing but a set of sets, i.e. the elements are themselves sets. This question leads to the famous paradox named after Bertrand Russel, which stated in non-abstract words is known as the Barber Paradox: The male barber who shaves all men who don't shave themselves has to shave himself if and only if he does not shave himself. To learn more about these paradoxes, refer to this Wikipedia article.

Operations on Sets: Algebra

Students often think of algebra as a set of mechanical rules to "calculate things". A more modern and more accurate definition of algebra would be the study of relations and relationships between objects. These relations often come in the form of special operations and maps. We introduce these two notions in what follows.

Maps. Given two sets A and B, a map f from A to B is informally a way of associating elements in B to elements in A. One can also think of it as a way of transforming elements in A to elements in B. The notation for such a map is f : A → B.
Formally, such a map is a subset S_f of the cartesian product A x B, where every element a in A appears in exactly one pair (a, f(a)) ∈ S_f, where the element f(a) ∈ B is called the image of a.
In practice, it is simply the data of one element f(a) ∈ B for each element a &isin A.

Let us consider an example to clarify this seemingly obscure definition. Consider the sets A = {a, b, c} and B = {1, 2, 3}, then the following diagram defines a map f : A → B:

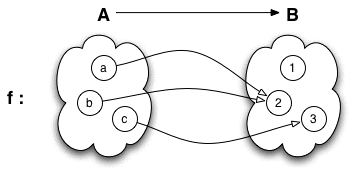
such that f(a) = 2, f(b) = 2 and f(c) = 3. Notice that while one can have f(a) = f(b) for two different elements a and b, it is not allowed to have f(a) = x and f(a) = y for two distinct elements x and y, by definition.

Operations. Operations, more precisely binary operations here, are special types of maps. Given a set A, a binary operation @ is a map @ : A x A → A. In other words, it is a device that takes pairs of elements in A as an input and outputs another element in A. One usually writes a @ b for @((a, b)), where a and b are elements in A.

For example, let A be the set {a, b, c} then one can define a binary operation on A by filling the entries of a 3 by 3 table with elements in A, such that x @ y lies at the intersection of row x and column y. For example, the following table defines such an operation:

@	a	b	c
a	a	b	c
b	b	b	a
c	c	b	c

In this case, a @ b = b, c @ a = c and b @ b = b for example.

Now suppose that we have two sets A and B, and two operations @ A x A → A and # B x B → B. Suppose we also have a map f : A → B. Given two elements in A, call them x and y, one can do the following actions.

• First, we can combine x and y and look at x @ y. This is another element in A and we can transform that into an element in B with f by calulating f(x @ y)..
• Second, one can transform x and y into elements in B by taking f(x) and f(y). One can them combine these two elements in B into yet another element in B by computing f(x) # f(y)

In general, there is no reason to expect that both recipes agree. In other words, there is no reason to have f(x @ y) = f(x) # f(y). Maps that satisfies this property are special and are called homomorphisms or simply morphisms. One also says of such a map that it agrees with the operations or that it is compatible with them. Given any random sets with operations, there might not be any homomorphism between them at all!
Another way of writing the defining property of morphisms is to say that they make the following diagram commute, i.e. the different calculation paths given by following the arrows all agree on the result:


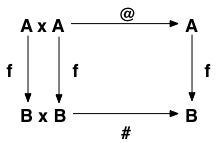
These kinds of maps are at the heart of abstract algebra where one studies sets with special kinds of operations and homomorphisms between them.

Which ones of the following pairs form a pair of a set with a binary operation on it.

• The natural numbers with addition? With multiplication? With substraction? What about division?
• Rational numbers with multiplication? And division? What is special with 0?
• The set of students in a classroom and the map that sends a pair of students to all the friends they have in common in that classroom? How to change the set and the map a little bit so that it becomes a binary operation? (Think of the set of subsets of students).

Show that both the real numbers with addition, call them (R, +) and the real numbers with multiplication, (R, x), form twp pairs of a set with a binary operation. Do the same thing with the positive real numbers with multiplication.

• Show that the map that sends a real number number to its double is a morphism of sets with operations from (R, +) to (R, +). Can you find other examples? How about the map that sends a number to itself plus 5?
• Show that the Exponential map is morphism of sets with operations for the right operations (The set is obviously that of the real numbers. Look at the operations you have, and see what happens when you apply the exponential).
• Do the same thing with the Logarithm function.

In the following section, we continue investigating sets and operations and show how this all leads to the definition of a group.