Permutations

In this section, we are going to take the abstraction a step further an get a little bit closer to abstract groups by considering symmetries as permutations.

Consider the reflection XA as we defined it earlier:

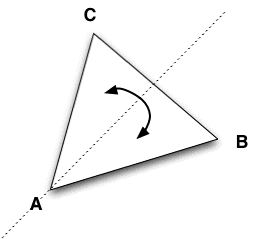
This reflection keeps A where it is, swtiches B and C and it is completely identified by that. In other words it is simply a permutation of the vertices of the triangle: it shuffles them so that each vertex goes to one and only one new vertex, and no two vertices go the same new one. In other words, we could summarize or write this symmetry in a much more concise fashion by writing something like this:

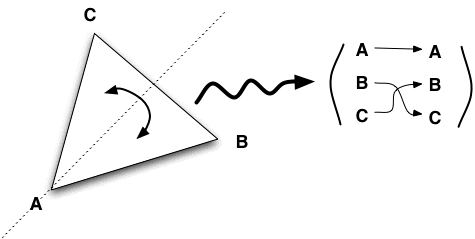
This way, we do not need to draw a triangle every time we need to describe what that symmetry does and we are not loosing any information by doing so -- i.e. there is no possible confusion when communicating the information this way.

In fact, we can do even better and get rid of the arrows. Doing so we get the standard mathematical notation to write a permutations:

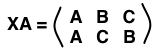
Using this notation, the other symmetries are as easy to write. For example, we for R1 and XB we have:


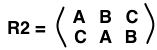
What happends to the composition of symmetries in this notation? We already know that XB @ XA = R2. Can we see that easily with our new notation? Well let's look at XB @ XA. Remember we do XA first then XB. XA takes A to A and then XA takes that A to C. So we have the following sequence:

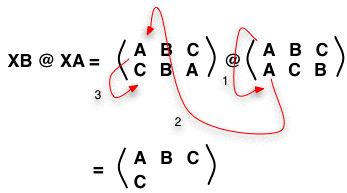
As to B, XA takes it to C and then XB takes that C to A again:
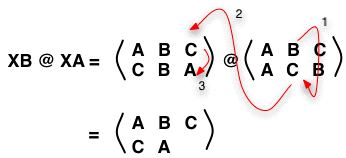
If we carry on the next step and following the path of C we get the composition:

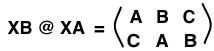
Which is indeed equal to R2 in this notation.

Write down XC @ XA and check that XC @ XB = R2 as well.

Now given a random permutation of the three letters A, B and C, call it a 3-permutation, can one always find a symmetry of the triangle that is described by this permutation? For example, is there any symmetry that corresponds to ?
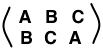
Well, we have counted 6 symmetries for the triangle: the trivial one, R1 and R2 and the 3 reflections XA, XB and XC. These were all of them and in fact: if we compose any two symmetries in that list, we have found that we obtain another symmetry in that list.
Now each one of these symmetries gives a different permutation, so if our question permutation is one of those 6 permutations, we know it comes from one of the symmetries. But how many permutations of A, B and C are there all in all?

Let us count how many ways we can permute A, B and C: A has to go to either A, B or C and so we have 3 possibilities for the image of A. For each one of those possibilities, B can only go to two letters now. Indeed, if we know that A goes to B, then B can only go to A or C, but not B. This is because no two letters can go to the same one under the permutation. So for each one of those 3 possibilities for A, we have 2 possibilities for B. At that point, there is only 1 possibility left for C and it is the only remaining letter.

This shows that are exactly 3 x 2 x 1 = 6 ways of permuting the letters A, B and C. We call this number 3! and we pronounce it factorial 3. This notation is so handy that we obviously do not restrict its usage to the number 3 and we say for example that factorial 5 is 5! = 5 x 4 x 3 x 2 x 1 = 120.

In summary we have 6 permutations in total, 6 of which come from symmetries of the triangle. In other words, every 3-permutation is the permutation associated to a symmetry of the triangle! Is the same true about the square?

Recall that we found 8 symmetries for the square: the trivial one, 3 rotations (90*, 180* and 270*) and 4 reflections (2 for the diagonals and 2 for the sides). Again, each one of these symmetries gives a different 4-permutation and we can ask the same question as before: given a random 4-permutation, is it always the permutation associated to a symmetry of the square?

To answer this question we can once again count how many 4-permutations there are in total, and the answer is obviously 4! = 4 x 3 x 2 x 1 = 24. So we have 24 possible permutations, only 8 of which come from actual symmetries of the square! For example there is no way of connection these two corner labeling using only rotations and reflections:


One other interesting fact is the following: Both the set of all permutations and that of symmetries of the square satisfy the properties we listed in the previous section. Namely, that they both contain the trivial permutation/transformation; when we compose two general permutations we get a general permutation and when we compose two permutations corresponding to a symmetry we get a permutation corresponding to a symmetry as well (the composition symmetry); the elements in both sets all have permutations within that same set that cancels them out after composition. We will see that this corresponds to the notion of a sub-group sitting inside a bigger group: the nth-symmetric group or total group of n-permutations.

Before we get to that though, we are going to spend a little more time talking about permutations.

Towards The Symmetric Group

Let us re-consider 4-permutations and their notations. Instead of writing A, B, C and D, we will write numbers 1 through 4. The reasom for this is first that the notation is more general and that it turns out to be easier on the notation for more advanced topics, and second, that it leads to easier generalization to n-permuations -- especially for n greater than 26!

Some permutations only swap two elements and leave all the other ones unchanged. While it may sound at first as if they were not very interesting, it turns out that these permutations are fundamental. We call them transpositions and an example would be the reflection symmetries in the triangle. If one composes them with themselves, they cancel out to the trivial permutation. These permutation are so fundamental that we have a special notation for them that is even more concise than the general one. Here is an example: The permutation swaps 1 and 2, and leaves everything else unchanged. We will write such a transposition as (1 2), meaning 1 goes to 2, 2 goes to 1 and everything else is unchanged. Notice that in this notation it is implied that the transposition is a 4-permutation. When using this notation, the context should always make it clear what is meant by "everything else" (here: 3 and 4).
Notice that we with the way we defined, both (1 2) and (2 1) refer to the same permutation.

Another fundamental type of permutation happens to also be a natural generilaztion to transpositions. We call them cycles because they cycle elements. An n-cycle is a permutation that takes i₁ to i₂, i₂ to i₃, ... , i_n-1 to i_n, i_n back to i₁ and leaves everything else unchanged (here i₁ to i_n are elements in the set of elements we are permuting -- {1, 2, 3, 4} in our examples). We write such a permutation (i₁ i₂ ... i_n).
For example the 2-cyle (1 2) is nothing but the permutation that swaps 1 and 2, and the 3-cycle (1 3 4) is the permutation that takes 1 to 3, 3 to 4 and 4 to 1, i.e (2 is unchanged).
Notice that here again (1 3 4) = (3 4 1) = (4 1 3) are all the same permutation, while (1 4 3) is a different one.
Also, (1) = (1 1) = (2) = (3) (etc...) are all the same permutation: the trivial one!

This new notation would not be very useful if it did not allow us to calculate compositions easily. Fortunately there is and the process is similar to what we had before. We show how to calculate the composition of (1 2 3) with (12). With cycles, one usually omits any composition symbol and simply writes (1 2 3) (1 2) for the composition permutation that applies (1 2) first, then (1 2 3). The technique we show breaks down the composition into cycles as we show now:

• Let us look at what happens to 1. The first permutation takes 1 to 2, and then the second one takes that 2 to 3. So under the composition, 1 goes to 3.
• Next, we look at what happens to 3 next. The first permutation takes 3 to 3 (it leaves in unchanged) and then the second one takes 3 to 1. So under the composition, 3 goes back to 1. And we have completed a cycle.
• We can now look at the other numbers, starting by 2 for example. The first permutation takes 2 to 1 and then the second one takes that 1 back to 2. The composition leaves 2 unchanged.
• The composition leaves 4 unchanged, obviously, because neither permations actually move 4.

In summary we have showed that (1 2 3) (1 2) = (1 3).

In general, we can use the previous technique to write a composition of permutations as composition of disjoint cycles. Let us explain what we mean by that. First, notice that for example (1 3) (2 4) = (2 4) (1 3). We say that those two cycles (they are transpositions in particular as you now know) are disjoint, meaning they permute two disjoint subsets of elements: the left-most ones swaps 1 and 3, while the second one swaps 2 and 4. The two subsets {1, 3} and {2, 4} are disjoint, they do not share any elements.
Disjoint cycles always commute: the order in which we compose them does not matter, we always get the same answer.

Now given two permutions like (1 2 3) and (1 2), we can see that these are not disjoint as they both change the 2's. In fact, while (1 2 3) (1 2) = (1 3), (1 2) (1 2 3) = (2 3)!

We show now on an example how to re-write a composition of non disjoint permutations into a composition of disjoint cycles which is equal to it. Consider the composition (1 2 3) (1 2 4). These two cycles are not disjoint but the following algorithm will allow us to rewrite it as a disjoint composition:

• Start with 1. The first permutation takes 1 to 2 and the second one takes that 2 to 3. We write (1 2 3) (1 2 4) = (1 3 ?
• Next we lool at 3. The first permutation takes 3 to 3, and then we take 3 to 1 and we have completed a cycle. We write (1 2 3) (1 2 4) = (1 3) ?
• After we complete a cycle, we start another cycle with the next free number. In this case, with start with 2. We write (1 2 3) (1 2 4) = (1 3) (2 ?
• The first permutation takes 2 to 4, and then the second one takes that 4 to 4. We write (1 2 3) (1 2 4) = (1 3) (2 4 ?
• Finally, the first permutation takes 4 to 1 and the second one takes 1 to 2 and we have completed a cycle. We write (1 2 3) (1 2 4) = (1 3) (2 4).
• There are no remaining numbers and we are done!

This shows that the two permutations (1 2 3) (1 2 4) and (1 3) (2 4) are equal, but the second one is the composition of two disjoint cycles. In some sense, that second expression is nicer because it breaks the original composition permutation down into its main "core components". We call it the disjoint cycle decomposition.

Here is another example. We calculate the decomposition for (1 2 3) (1 3).

• Start with 1. The first permutation takes 1 to 3 and the second one takes that 3 to back to 1. We finished a cycle which happens to be a trivial cycle: 1 goes to 1. We write (1 2 3) (1 3) = (1) ?.
• Next we lool at the first free number, i.e. 2. The first permutation takes 2 to 2, and then we take 2 to 3. We write (1 2 3) (1 3) = (1) (2 3 ?.
• Next we look at 3. The first permutation takes 3 to 1 and then second one takes that 1 to 2, and we have completed a cycle. We write (1 2 3) (1 3) = (1) (2 3).
• There are not numbers left and this we are done. Notice that (1) is just the trivial permutation: it takes 1 to 1 and leaves everything else unchanged! Now if we compose the trivial permutation with any other one, we obviously get that same permutation back. And thus we can simply our expression to (1 2 3) (1 3) = (2 3).

Generators

Remember that in the case of the triangle, there were exactly 6 symmetries and exactly 6 permutations of the set {1, 2, 3}, and each symmetry correponds to exactly one permutation.
Also, we showed that XA and XB generated all those permutations. Now identifying A, B and C with 1, 2 and 3 respectively, XA corresponds to (2 3) and XB to (1 3). This shows that those two transpositions generate all possible 3-permutations. Let us recall that this means that if we add the trivial permutation and take all the combinations of (multiple) compositions of those two transpositions, we get all the 3-permutations (we will later give a slightly more general definition of the word generating later). Let us check that they do generate all those permutations:

• (1 2 3) is the composition (2 3) (1 3)
• (1 3 2) is the composition (1 3) (2 3)
• (1 2) is (1 3) (1 2 3) = (1 3) (2 3) (1 3)
• (1 3) is just (1 3)
• (2 3) is also just (2 3)

And thus every non trivial 3-permutation can be indeed written as a composition of the two claimed generators. In fact we could rename all the corners and show the neater fact that (1 2) and (1 3) are also generators.

In the case of the square, we need to look at 4-permutations by identifying A, B, C and D with 1, 2, 3 and 4 respecively.

Show that the rotations correspond in that identification to the permutations (1 2 3 4), (1 2 3 4) (1 2 3 4) = (1 3) (2 4), (1 2 3 4) (1 2 3 4) (1 2 3 4) = (1 4 3 2); the diagonal reflections to (2 4) and (1 3); and the other reflections to (1 2) (3 4) and (1 4) (2 3).

We already know that the set of permutations listed in the question does not generate the whole set of 4-permutations. Mimicking the triangle case, one can wonder whether (1 2), (1 3) and (1 4) do generate the whole set. The answer is yes and it turns out this is a very general result, but we skip the derivation in here. See the references for more information about the symmetric group.

• One can show that any permutation (and not just a composition of cycles) can be written as a (multiple) composition of disjoint cycles. Follow what happens to 1, 2, 3 and 4 under the permutation , indentify the cycles and write the permutation as a composition of disjoint cycles.
• One can show in fact that one can always write any permutation as a (multiple) composition of (non-necessarily disjoint) transpositions. Try to write (1 2 3 4) as a composition of transpositions.