Symmetries as Sets with Special Operations
When we studied the symmetries of an equilateral triangle, we showed that we could list all of those in a list. According to our definition, this means that those symmetries form a set, call it
ST. Also, given two symmetries one could compose them and get yet another symmetry: the composition naturally gives
ST the structure of a set with an operation
@ : ST x ST → ST.
The fact the elements of the set are
transformations of the triangle and that the operation is nothing but the natural composition of transformations means that that operation has some very special properties.
First of all, let us consider the following example. Remember that we showed that
R2 @ XA = XB:

But now, remember that
R2 = R1 @ R1 so we can rewrite that equation as
(R1 @ R1) @ XA = XB. The parenthesis are here to show that we first compose
R1 with
R1, and then compose that new transformation with
XA. What happens if we consider
R1 @ (R1 @ XA)?
If the composition sign were a "+" then one knows that expressions like
(2 + 5) + 3 and
2 + (5 + 3) are equal. One says that "+" does not care as to what order we associate expressions involving more than 2 terms. In fact, we also have more complicated equalities like
(2 + 3) + (4 + 5) = (2 + (3 + (4 + 5))). For this reason, we can write expressions like that simply as
2 + 3 + 4 + 5 and get rid of the parenthesese.
If the composition sign were a "÷" sign, things would be different. Indeed, while
(2 ÷ 2) ÷ 2 = 1/2 one has that
2 ÷ (2 ÷ 2) = 2. In this case, an expression like
2 ÷ 2 ÷ does not make any sense at all. The parenthesese here are fundamental and how one puts parenthesese in that expression, one says that one
associates the expression, makes the result change dramatically.
In this example though, we do have that
(R1 @ R1) @ XA = XB = R1 @ (R2 @ XA) as one can check with a sequence of diagrams. In fact, this is also true because of the definition of the composition of transformation. In either case, we simply apply
XA,
R1 and then
R1 to the triangle. In fact, this is not specific to the particular expression but is true in general for all expression of the sort involving compositions of transformations. We say that that composition is
associative.
Associativity: In views of the previous discussion, we have the following definition. We say that an operation
# on a set
X is
associative if the following holds: for all
x,
y and
z elements in
X we have the following equality:
x # (y # z) = (x # y) # z In which case one simply writes
x # y # z

Which ones of the following operations are associative.
- Addition on the real numbers. Multiplication on the positive real numbers.
- Division on the non-zero real numbers.
- The operations defined by the following tables:
| * | a | b | c |
| a | a | b | c |
| b | b | b | a |
| c | c | b | c |
| # | a | b | c |
| a | a | b | c |
| b | b | c | a |
| c | c | a | b |
Another special property of
ST is the existence of a particular element with a very special role: the
trivial transformation. This transformation is such that when it is composed with any other transformation it leaves it
identically unchanged. This motivates the following definition:
Identity: An
identity for an operation
# on a set
X is an element
e of
X such that for all
x ∈ X we have
x # e = e # x = x
One natural question that arises from that definition is whether such an identity element is unique if it exists. In other words, can there be two distinct elements that behave like an identity for the operation? The following question shows the answer is
negative. For this reason, we call such an identity element
The identity.

Suppose an operation
# on
X has two identity elements
e and
f. Use the identity property for both
e and
f to simplify
e # f into two different expressions, and conclude that
e = f necessarily.
Finally, recall that for every symmetry of the triangle, there was another symmetry that canceled it out. In other words, the symmetries are
reversible transformations, one can always undo them. The following definition captures this idea.
Inverses: Let
# be an operation on
X with identity
e, and let
x be an element in
X. An
inverse for
x under
# is an element
y ∈ X such that:
x # y = y # x = e
This defintion means that an inverse for
x is an element that cancels it out, on
both sides.
Once again, a pair of natural question arise from this definition. First, is such an inverse element unique if it exists; then second, whether it is enough in the definition to ask for cancelation on one side only. In other words, does
x # y = e automatically imply that
y # x = e also? The following questions guide you through studying these questions.

Let
X,
# and
e as in the previous definition but assume that
# is
associative. Now let
x ∈ X with two inverses
y and
z. In other words,
x # y = y # x = e and
x # z = z # x = e. Show that
z = z # (x # y) = (z # x) # y and conclude that
z = y and hence that an inverse under an
associative operation is
unique if it exists.
Notice that the fact that the operation was associative was crucial in the proof. In this case we write
x-1 for the unqiue inverse to
x.
We now show that in some special cases, one only needs to ask for one-sided inverses to get both sides automatically. The proof of our statement is a little more involved in that it involves some notions of set theory we haven't discussed here. For an introduction to these notions, the reader can refer to the links on the conclusion page.

Here again, let
X,
# and
e as in the previous definition, but this time assume that
X is
finite, i.e. it only has finitely many elements, and that
# is
associative. Now let
x ∈ X and
y ∈ X such that
x # y = e. Consider the map
f : X → X defined by
f(a) = y # a for
a ∈ X.
- Show that f is one-to-one, a.k.a injective, by using an associativity trick on x # f(a)
- Deduce that f is also onto because X is finite.
- Deduce now that the previous statement implies that there exists an element z &isin X with y # z = e.
- Show that x = x # (y # z) implies that x = z and y # x = e.
In other words, in a finite set and under an associative operation,
x # y = e implies that
y # x = e.
Groups, Finally!
We can now finally give the definition of an abstract group and we have provided all the background necessary to making this definition completely transparent:
Group: A group is a set
G with a binary operation
# : G x G → G such that:
- The operation # is associative.
- It has an identity element (and hence it has exactly one).
- Every element in G has an inverse under # (and hence a uniquely defined inverse).

Which one of these sets with operations are Groups?
- The natural numbers with addition? With multiplication? How about substraction?
- Same question with the rational numbers?
- The operations defined by the following tables?
| * | a | b | c |
| a | a | b | c |
| b | b | b | a |
| c | c | b | c |
| # | a | b | c |
| a | a | b | c |
| b | b | c | a |
| c | c | a | b |

Let
M be the set of expressions of the form
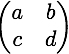
where
a,
b,
c and
d are real numbers. Define the binary operation
+ on
M by the following expression:

.
Show that this operation makes
M into a group. What is the identity in this case?
Consider now
O to be the subset of
M of elements
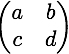
such that
a d - bc ≠ 0, with operation
* defined by:

.
Show that this makes
O into a group with identity
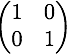
.
Giving these definitions is only the begining of a long and beautiful journey through algebra with connections to geometry, physics, analysic and so many other areas of mathematics.
Studying the consequences of this definition would take many different writeups like this one and is beyond the scope of this introduction.
The conclusion section offers a few links and pointers as to what one could look into next. We hope the reader feels comfortable tackling those texts after having read this one.