Data
We computed eigenfunctions 0-series as well as those in the 4/3-series
born at level 0, all for the standard Vicsek set (n = 2). Often
it's easier to look at plots restricted to a diagonal. All of the plots are for
the 4th level graph approximation (m=4):
For higher n we only have diagonal plots:
Restriction to the Diagonal
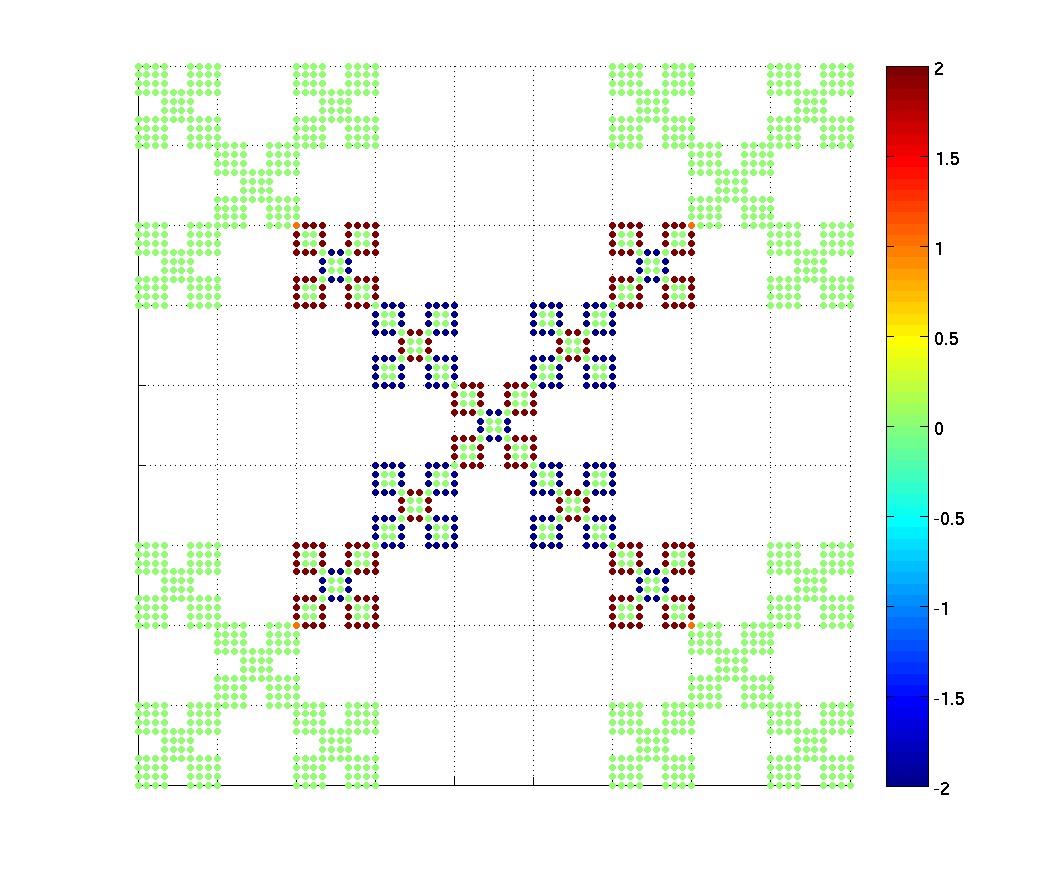
Eigenfunctions in the span of the 0-series are uniquely determined by
their values on an "arm" (a line from the center of the Vicsek set to on
of the corners). On a graph approximation, functions in the span of the
0-series whose values on an arm are all zeros and a single one take on a
surprisingly simple form (for instance they take on at most 5 values).
Here is a gallery (pdf) of these functions for
n=2, m=4.
Limit as n goes to infinity
As n increases, the Vicsek set looks more and more like two
crossed lines. For this reason, we conjecture that the eigenfunctions
should converge to trigonometric functions. This is supported by our
numerical results. For instance, here is a plot of the first 0-series
eigenfunction (restricted to the diagonal) for various values of
n:

