Decomposition

SG²

Decomposition

What exactly is irregular decomposition, and why do we use it? Irregular decomposition is when some cells of the graph a finer approximation (a deeper level, so to say) than other cells. It's easier to give a picture:


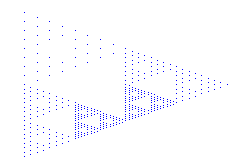
Irregular decomposition of the SG around [0,1]	Regular decomposition. Look how many more points there are to deal with!

Let's say we are very interested in a certain point on the SG²; perhaps we want to approximate a delta mass there. If we were doing regular decomposition, and wanted a fine approximation, we might make one point on the gasket very large, and decompose out to level 7. The number of points in this case will be on the order of 3⁷; quite a headache for your computer. Irregular decomposition of the cells allows us to control which points we want a fine detail at, and which points we can all but ignore.

To implement irregular decomposition, we use a similar system to that of Kevin Coletta's (website). The decomposition is stored in a list of words, and each word corresponds to a cell in our addressing system. For more about the addressing system, click here (external link). Kevin Coletta's code provides many functions to decompose the SG, and I have included functions to create the cross-products of these lists. The example above can be formed as follows:

> W := reg_wordlist(1); W := zoom_wordlist(W,[0,1],1); W := zoom_wordlist(W,[0,1],1);

And the next code would make the wordlist W into a product of itself:

> W := wordlist_makeprod(W);