SG2

Green's Function

Home
Up
Pluribiharmonic Functions
Splines
Decomposition
Finite Element Method
Green's Function
Poisson Kernel
Differential Operators
Eigenvalues

 One of the more interesting functions on SG2 is the Green's Function, G(x,y). Green's function is important, as it inverts the Laplacian operator on dom(D) mod harmonic functions (the kernel of the Laplacian). It solves the Poisson equation under Dirichlet conditions:
 
Du = f
u ||V0 = 0
 

is solved by

u(x) = ó
õ

SG2 		 G(x,y) f(y) dy

Green's function on SG2 is known to have the following properties:

bulletIt is zero on the boundary
bulletFixing y, Green's function is harmonic everywhere except at x=y, where it has a singularity. In other words, x ¹ y, DG(x,y) = 0
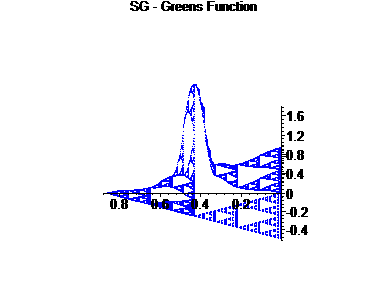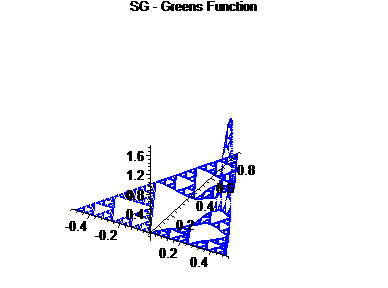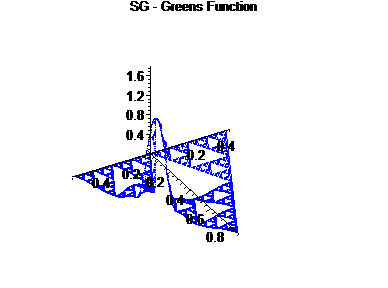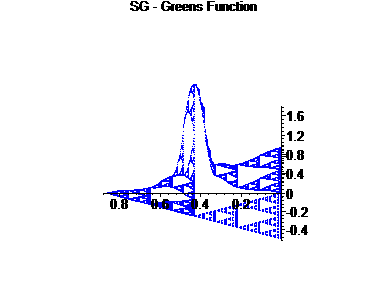
bulletTheoretically, Green's function should obey a power law: G(x,y) £ c d(x,y) d¢-1, where d(x,y) is the metric and d¢ is the dimension of SG2

Unlike other functions, such as the heat kernel or pluriharmonic functions, Green's function changes drastically from the case of SG to that of SG2. For example, comparing the unit interval to the square, the Green's function goes from having a point of non-differentiability at x=y to having a pole at its singularity. On the SG and SG2, we expect to have a very similar situation, with a pole at the singularity for SG.

We use the FEM to approximate a solution of Green's Function on the SG2, by using the fact that DG = 0 except at the singularity. We set q=0 in (3) and F=0 except at the point in the spline which corresponds to the singularity; there, F=1. Thus, the approximation is:

 
E ·c = F
{E}i,j = E(qi, qj)
{F}i = 0, qi(y) = 0
{F}j = 0, qj(y) = 1
 
(4)

In order to display the solutions to these equations, we graphed the picture of y¢ÄSG and SG Äy¢¢. In the following graphs, we show the approximations of G(x,y) for various fixed y.