Differential Operators

SG²

One of the most interesting things about the SG² is the possibility of more differential operators. The standard Laplacian that has been used throughout the paper is actually simply the sum of the two factor Laplacians: D = Dў+ Dўў. A natural question for the product setting is the existence of a wider class, such as D = Dў+ aDўў. The question is very difficult; for example, consider for a = -1 the solution of the Poisson equation for a function f. Let u_i represent an eigenfunction.

Df =

f_ij u_i u_j = g

f_ij u_i u_j =

f_ij (l_i - l_j) u_i u_j =

g_ij u_i u_j

f_ij =

g_ijl_i - l_j

Notice that, in the case where some eigenvalues have a high multiplicity (which we are in), there will be many cases where l_i = l_j, and we are dividing by zero. Therefore, we ask the question of whether or not there exists a constant c s.t. [(l_i)/(l_j)] № c; aka, is there a gap in the in the structure of the quotients of the eigenvalues?

From the methods of spectral decimation, for each eigenvalue l, l = [ 3/2] lim_{m
®Ґ} 5^m l_m, where l_m₀ = 2, 3, 5 and l_m+1 = f_± l_m where only a finite number of f₊ are applied. f_± is defined as

f_±(x) =

5 ±

25 - 4x

Notice that f₊ is orientation-reversing, and has a fixed point at 4. f_- is orientation preserving and has a fixed point at 0. Suppose the last f₊ is at index M-1. Then l_m = f₊(l_m-1) О [ 3, 5 ] and l = [ 3/2] 5^k Y(l_m) where Y(x) = lim_{n®
Ґ} 5ⁿ f_-ⁿ(x). So,

lў

= 5^k

Y(l_m)

Y(lў_mў)

, (-Ґ < k < Ґ)

Note that

Y(l_m)

Y(lў_mў)

й
л

Y(3)

Y(5)

Y(3)

щ
ы

So, as long as

ж
и

Y(5)

Y(3)

ц
ш

< 5

there will be gaps between [(Y(5))/(Y(3))] and [(5 Y(3))/(Y(5))]. Computationally, [(Y(5))/(Y(3))]² = 4.248176580, and a gap should be located at [2.0611,2.4258].

We fix a = 2.25, and analyze the graphs of the Green's Function for this differential operator.

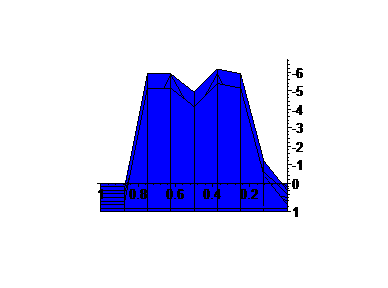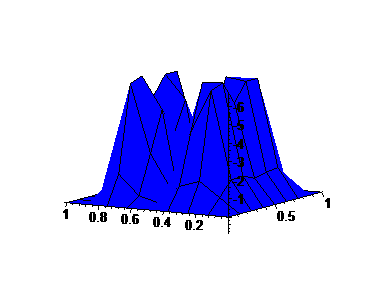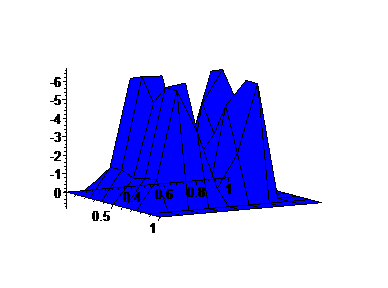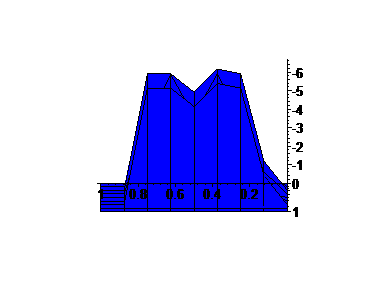
The first graph is G(x,[0,1]) for a = 2.25, with only a piece, [0,1] ДSG displayed.

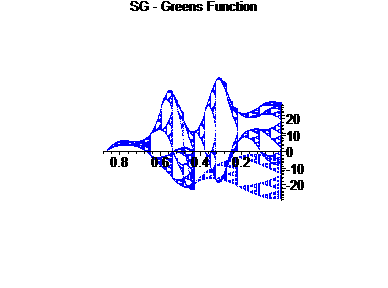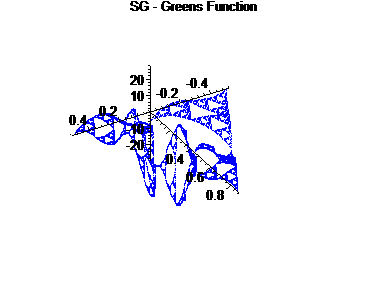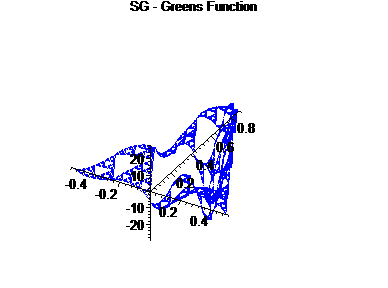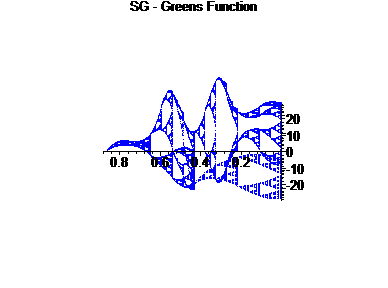
For the second graph, we examine the right ``edge" of the first factor crossed with the right edge of the second factor, to form a 2-d graph.

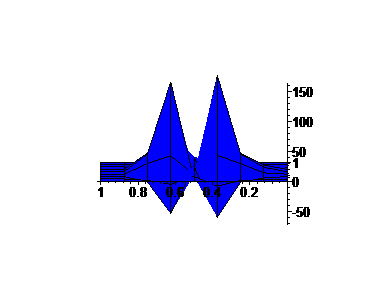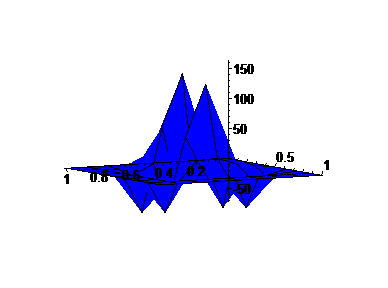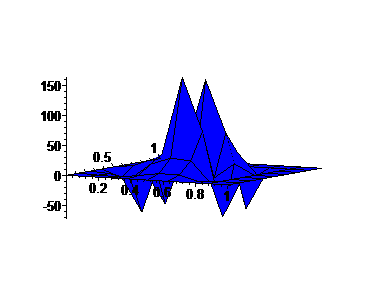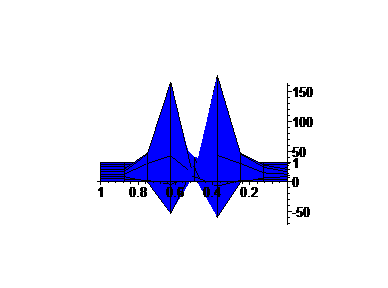
We fix a = 2.2, and analyze the graphs of the Green's Function for this differential operator.

The first graph is G(x,[0,1]) for a = 2.25, with only a piece, [0,1] ДSG displayed.

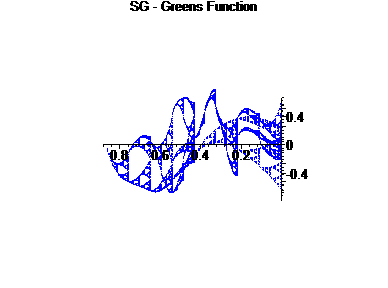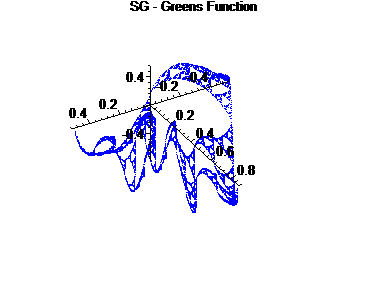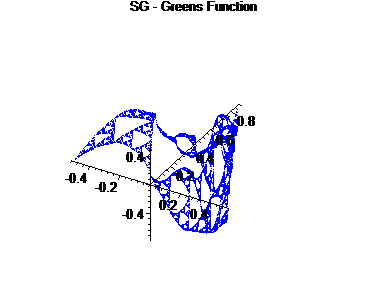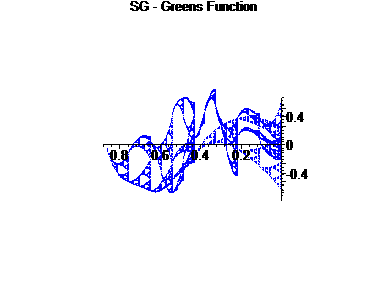
For the second graph, we examine the right ``edge" of the first factor crossed with the right edge of the second factor, to form a 2-d graph.