SG2

I have divided this page into the following subtopics:
- Existence of gaps in the eigenvalues
- Pictures of the ratios of eigenvalues
- Development of the eigenvalue ratios
The eigenvalues of the Laplacian are very important. For reasons discussed on the Differential Operators page, it is important for gaps to exist in the quotients of the eigenvalues because this allows for the existence of operators of the form D = D¢+ |c|D¢¢. The proof of the existence of gaps follows:
From the methods of spectral decimation, for each eigenvalue l, l = [ 3/2] limm ®¥ 5m lm, where lm0 = 2, 3, 5 and lm+1 = f± lm where only a finite number of f+ are applied. f± is defined as
|
Notice that f+ is orientation-reversing, and has a fixed point at 4. f- is orientation preserving and has a fixed point at 0. Suppose the last f+ is at index M-1. Then lm = f+(lm-1) Î [ 3, 5 ] and l = [ 3/2] 5k Y(lm) where Y(x) = limn® ¥ 5n f-n(x). So,
|
Note that
|
So, as long as
|
there will be gaps between [(Y(5))/(Y(3))] and [(5 Y(3))/(Y(5))]. Computationally, [(Y(5))/(Y(3))]2 = 4.248176580, and a gap should be located at [2.0611,2.4258].
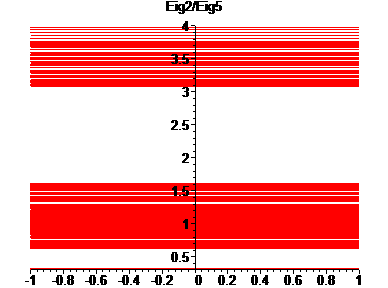
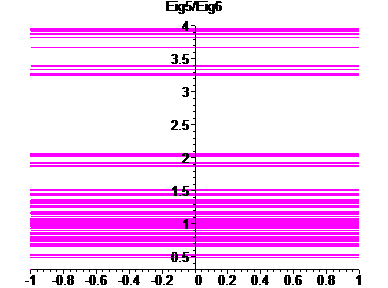
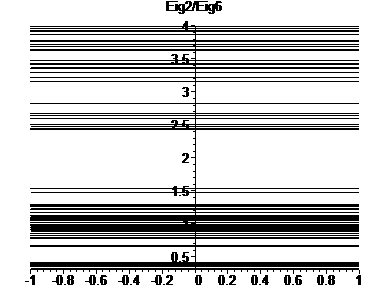
Computationally, we can also see that other gaps exist. Following is the graph of the quotient of the eigenvalues:
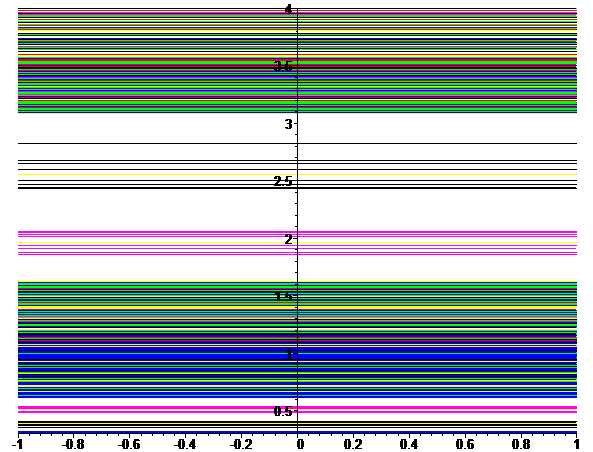
Each vertical line represents a quotient of eigenvalues. It is colored as follows:
| Value of Base Eigenvalues: | Color: |
| 2, 2 | blue |
| 5, 5 | green |
| 6, 6 | yellow |
| 2, 5 | red |
| 5, 6 | magenta |
| 2, 6 | black |
Clicking on the above links will take you to a graph of quotients of just those base eigenvalues.
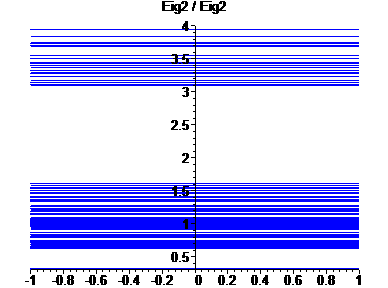 |
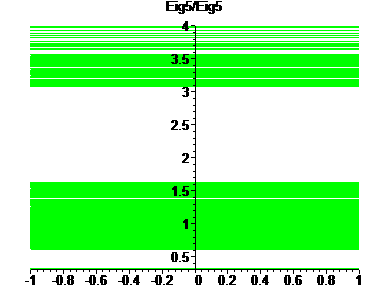 |
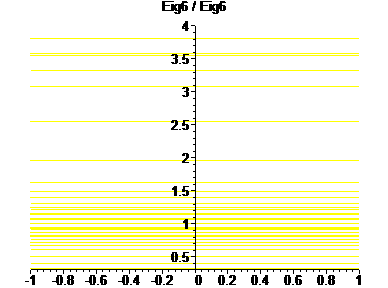 |
 |
 |
 |
Development of Ratios
One obvious question is the existence of true bands, i.e., intervals that become filled in with the limit of all the ratios. From the above pictures, it appears obvious that these intervals exist - especially when the base eigenvalue 5 is involved. Existence of bands is less obvious with other base eigenvalues - most noticably eigenvalue 6, as the eigenvalue ratios do not even cluster around 1! One thing that is being examined is the development of the graphs of the ratios as more and more eigenvalues are added. For example, the following graph displays the development of the ratios of the 5-series. I added 10 eigenvalues at a time, progressing to the right, up to 50 eigenvalues, and displayed all of the ratios. One can then see what intervals fill up the fastest as more and more eigenvalues are considered:
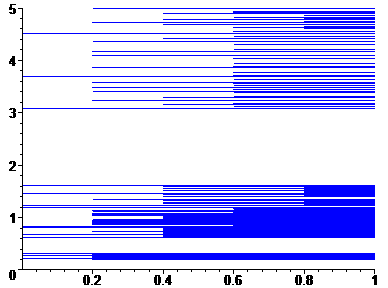
We are working on a fuller understanding and analysis of this picture and the interval question.