|
Lionel LevineProfessorDepartment of Mathematics Cornell University |
|
CV | Research | Papers | Talks | Teaching | Gallery | Fun! | Contact
New Course: Math for AI Safety (Fall 2024)
Hello, I'm Lionel! I study abelian networks. These are interacting particle systems whose final state does not depend on the order of interactions. From another point of view, they are systems of communicating automata that pass messages to perform an asynchronous computation. I was inspired to work in this area by Deepak Dhar, Cris Moore, Yuval Peres, and Jim Propp.
If you want to learn a bit about this fascinating nexus of math, computer science, and statistical physics, I recommend starting with WHAT IS a sandpile? for a non-technical overview, and Laplacian growth, sandpiles, and scaling limits for a more recent survey.
Some highlights of my research are the scaling limit of the abelian sandpile in Z^2 where an Apollonian circle packing makes a surprise appearance, the devil's staircase for parallel chip-firing, refuting the density conjecture for sandpiles, logarithmic fluctuations for internal DLA, asynchronous circuits with integer input and output, fast simulation of growth models, a generalization of Knuth's formula for spanning trees, and word equations in uniquely divisible groups.
I thank Open Philanthropy, National Science Foundation, Sloan Foundation, Simons Foundation, and Institute for Advanced Study for supporting my research.

|

|

|

|
Papers and preprints (my papers on arXiv):
- Eliott Glazer et al.
FrontierMath: A benchmark for evaluating advanced mathematical reasoning in AI
- Rowan Hess and Lionel Levine
How to quantify the coherence of a set of beliefs
- Wilson Wu, John X. Morris and Lionel Levine
Do language models plan ahead for future tokens?
CoLM 2024
- Lionel Levine and Vittoria Silvestri
Universality conjectures for Activated Random Walk
Probability Surveys (2024) 21: 1-27
- Lionel Levine and Feng Liang
Exact sampling and fast mixing of Activated Random Walk
Electronic Journal of Probability (2024) 29:1--20
- Viktor Kiss, Lionel Levine, and Lilla Tóthmérész
The devil's staircase for chip-firing on random graphs and on graphons
Random Structures and Algorithms (2024)
- Lila Greco and Lionel Levine
Branching in a Markovian environment
Markov Processes and Related Fields (2023) 29(1):1--33
- Swee Hong Chan and Lionel Levine
Abelian networks IV. Dynamics of nonhalting networks
Memoirs of the American Mathematical Society (2022) 276, 1358
- Lionel Levine, Hanbaek Lyu and John Pike
Double jump phase transition in a random soliton cellular automaton
International Math Research Notices (2022) 665--727
- Lionel Levine and Vittoria Silvestri
How far do Activated Random Walkers spread from a single source?
Journal of Statistical Physics (2021) 185, 18
- Swee Hong Chan, Lila Greco, Lionel Levine, and Peter Li
- Random walks with local memory
Journal of Statistical Physics 184 (2021), Article 6, 28 pp.
- Lionel Levine and Vittoria Silvestri
How long does it take for internal DLA to forget its intitial profile?
Probability Theory and Related Fields (2019) 174:1219--1271
- Shirshendu Ganguly, Lionel Levine and Sourav Sarkar
Formation of large-scale random structure by competitive erosion
Annals of Probability (2019) 47:3649--3704
- Bob Hough, Daniel C. Jerison and Lionel Levine
Sandpiles on the square lattice
Communications in Mathematical Physics (2019) 367:33--87
- Daniel C. Jerison, Lionel Levine and John Pike
Mixing time and eigenvalues of the abelian sandpile Markov chain
Transactions of the American Mathematical Society (2019) 372:8307--8345
- Alexander E. Holroyd, Lionel Levine and Peter Winkler
Abelian logic gates
Combinatorics, Probability, and Computing (2019) 28:388--422
- Wilfried Huss, Lionel Levine and Ecaterina Sava-Huss
Interpolating between random walk and rotor walk
Random Structures & Algorithms (2018) 52:263--282
- Lionel Levine and Yuval Peres
Laplacian growth, sandpiles and scaling limits
Bulletin of the American Mathematical Society (2017) 54:355--382
- Shirshendu Ganguly, Lionel Levine, Yuval Peres and James Propp
Formation of an interface by competitive erosion
Probability Theory and Related Fields (2017) 168:455--509
- Elisabetta Candellero, Shirshendu Ganguly, Christopher Hoffman and Lionel Levine
Oil and water: a two-type internal aggregation model
Annals of Probability (2017) 45:4019--4070
- Lionel Levine, Wesley Pegden and Charles K. Smart
Apollonian structure of integer superharmonic matrices
Annals of Math (2017) 186:1--67
- Lionel Levine and
Ramis Movassagh
The gap of the area-weighted Motzkin spin chain is exponentially small
Journal of Physics A: Mathematical and Theoretical 50.25 (2017)
- Lionel Levine, Wesley Pegden and Charles K. Smart
Apollonian structure in the abelian sandpile
Geometric and Functional Analysis (2016) 26(1):306--336
- Benjamin Bond and Lionel Levine
Abelian networks III. The critical group
Journal of Algebraic Combinatorics (2016) 43:635--663
- Benjamin Bond and Lionel Levine
Abelian networks II. Halting on all inputs
Selecta Mathematica (2016) 22:319--340
- Benjamin Bond and Lionel Levine
Abelian networks I. Foundations and examples
SIAM Journal on Discrete Mathematics (2016) 30:856--874
- Matthew Farrell and Lionel Levine
CoEulerian graphs
Proceedings of the American Mathematical Society (2016) 144:2847--2860
- Matthew Farrell and Lionel Levine
Multi-Eulerian tours of directed graphs
Electronic Journal of Combinatorics (2016) 23:P2.21
- Lionel Levine, Mathav Murugan, Yuval Peres and
Baris
Ugurcan
The divisible sandpile at critical density
Annales Henri Poincare (2016) 17(7):1677-1711
- Laura Florescu, Lionel Levine and Yuval Peres
The range of a rotor walk
American Mathematical Monthly (2016) 123(7):627--642
- Lionel Levine
Threshold state and a conjecture of Poghosyan, Poghosyan, Priezzhev and Ruelle
Communications in Mathematical Physics (2015) 335(2):1003–-1017
- Louis J. Billera, Lionel Levine and Karola Mészáros
How to decompose a permutation into a pair of labeled Dyck paths by playing a game
Proceedings of the American Mathematical Society (2015) 143:1865-–1873
- David Jerison, Lionel Levine and Scott Sheffield
Internal DLA and the Gaussian free field
Duke Mathematical Journal (2014) 163(2):267–-308
- Lionel Levine and Yuval Peres
The looping constant of Z^d
Random Structures & Algorithms (2014) 45:1--13
- Laura Florescu, Shirshendu Ganguly, Lionel Levine and Yuval Peres
Escape rates for rotor walks in Z^d
SIAM Journal on Discrete Mathematics (2014) 28(1):323--334
- Lionel Levine, Scott Sheffield and Katherine E. Stange
A duality principle for selection games
Proceedings of the American Mathematical Society (2013) 141(12): 4349--4356
- Christopher J. Hillar, Lionel Levine and Darren Rhea
Equations solvable by radicals in a uniquely divisible group
Bulletin of the London Mathematical Society (2013) 45(1): 61--79
- Tobias Friedrich and Lionel Levine
Fast simulation of large-scale growth models
Random Structures & Algorithms (2013) 42: 185–-213
- David Jerison, Lionel Levine and Scott Sheffield
Internal DLA in higher dimensions
Electronic Journal of Probability (2013) 18(98): 1--14
- David Jerison, Lionel Levine and Scott Sheffield
Logarithmic fluctuations for internal DLA
Journal of the American Mathematical Society (2012) 25: 271--301
- Giuliano Giacaglia, Lionel Levine, James Propp and Linda Zayas-Palmer
Local-to-global principles for the hitting sequence of a rotor walk
Electronic Journal of Combinatorics (2012) 19: P5
- Lionel Levine
Sandpile groups and spanning trees of directed line graphs
Journal of Combinatorial Theory A (2011) 118: 350-–364
- Lionel Levine
Parallel chip-firing on the complete graph: devil's staircase and Poincaré rotation number
Ergodic Theory and Dynamical Systems (2011) 31: 891--910
- Wouter Kager and Lionel Levine
Rotor-router aggregation on the layered square lattice
Electronic Journal of Combinatorics (2010) 17: R152
- Anne Fey, Lionel Levine and David B. Wilson
Driving sandpiles to criticality and beyond
Physical Review Letters (2010) 104: 145703
- Anne Fey, Lionel Levine and David B. Wilson
The approach to criticality in sandpiles
Physical Review E (2010) 82: 031121
- Wouter Kager and Lionel Levine
Diamond Aggregation
Mathematical Proceedings of the Cambridge Philosophical Society (2010) 149: 351--372
- Anne Fey, Lionel Levine and Yuval
Peres
Growth rates and explosions in sandpiles
Journal of Statistical Physics (2010) 138: 143--159
- Lionel Levine and Yuval Peres
Scaling limits for internal aggregation models with multiple sources
Journal d'Analyse Mathematique (2010) 111: 151--219
- Itamar Landau and Lionel Levine
The rotor-router model on regular trees
Journal of Combinatorial Theory A (2009) 116: 421--433
- Lionel Levine and Yuval
Peres
Strong spherical asymptotics for rotor-router aggregation and the divisible sandpile
Potential Analysis 30 (2009), 1--27
- Lionel Levine
The sandpile group of a tree
European Journal of Combinatorics 30 (2009) 1026--1035
- Alexander E. Holroyd,
Lionel Levine,
Karola Mészáros,
Yuval Peres,
James Propp and
David B. Wilson
Chip-firing and rotor-routing on directed graphs
in In and Out of Equilibrium II, Progress in Probability vol. 60 (Birkhauser, 2008)
- Lionel Levine and Yuval Peres
Spherical asymptotics for the rotor-router model in Z^d
Indiana University Mathematics Journal 57 (2008), no. 1, 431--450
- Christopher J. Hillar and Lionel Levine
Polynomial recurrences and cyclic resultants
Proceedings of the American Mathematical Society 135 (2007), 1607--1618
- Lionel Levine
Fractal sequences and restricted Nim
Ars Combinatoria 80 (2006), 113--127
Expository notes:
- Lionel Levine and Katherine E. Stange
How to make the most of a shared meal: plan the last bite first.
American Mathematical Monthly 119 (2012) no. 7, 550--565
- Lionel Levine and James Propp
WHAT IS a sandpile?
Notices of the American Mathematical Society 57, (2010) no. 8, 976--979
- Lionel Levine and Yuval Peres
The rotor-router shape is spherical
Mathematical Intelligencer 27 (2005) no. 3, 9--11
- Lionel Levine
Fermat's little theorem: a proof by function iteration
Mathematics Magazine 72, no. 4 (1999), 308--309
Selected talks:
- Math for AI Safety (August 2024)
- CoEulerian graphs
- Halting problems for sandpiles and abelian networks: video
- Introduction to abelian networks: slides video
- The future of prediction (Math Awareness Public Lecture)
- Circles in the sand
- Logarithmic fluctuations from circularity
- An algebraic analogue of a formula of Knuth
- Chip-firing and a devil's staircase
- Obstacle problems and lattice growth models
Teaching:
- (upcoming) MATH 6720: Graduate Probability II, Spring 2025
- (current) MATH 7710: Topics in Probability: Math for AI Safety, Fall 2024
- MATH 1340: Strategy, Cooperation, and Conflict, Spring 2023
- MATH 6710: Graduate Probability I, Fall 2022
- MATH 7710: Topics in Probability: Limits of discrete random structures, Spring 2022
- MATH 6710: Graduate Probability I, Fall 2021
- MATH 1110: Calculus I, Fall 2021
- MATH 6720: Graduate Probability II, Spring 2021
- MATH 6710: Graduate Probability I, Fall 2020
- MATH 7710: Topics in Probability: Abelian Sandpiles and Abelian Networks, Fall 2020
- MATH 4210: Nonlinear Dynamics and Chaos, Spring 2020
- MATH 6720: Graduate Probability II, Spring 2020
- MATH 6710: Graduate Probability I, Fall 2019
- MATH 6720: Graduate Probability II, Spring 2018
- MATH 6720: Graduate Probability II, Spring 2017
- MATH 1340: Mathematics and Politics, Spring 2016
- MATH 4740: Stochastic Processes, Spring 2015
- MATH 6710: Probability I, Fall 2014
- MATH 4740: Stochastic Processes, Spring 2014
- MATH 4740: Stochastic Processes, Spring 2013
- MATH 7770: Topics in Probability: Laplacian Growth, Fall 2012
- 18.312 Algebraic
Combinatorics, Spring 2011
Some unpublished papers and notes:
- (with Yuval Peres) Internal erosion and the
exponent 3/4 describes how an unusual exponent arises from a very simple erosion process in one dimension. The proof we give
is due to Kingman and Volkov (2003), who thought of this not as an erosion process but as a model of a
gunfight (!)
- Orlik-Solomon Algebras of
Hyperplane Arrangements, an expository paper proving the basic theorem
of Orlik-Solomon and Brieskorn on the cohomology ring of the complement of
a complex arrangement, along with some remarks about the associated
combinatorics of the intersection lattice.
- My Ph.D. thesis, advised by Yuval Peres at Berkeley, used ideas from free boundary problems in PDE to prove limit shapes for both random and deterministic growth models. This topic has advanced a lot in the last fifteen years. Our article Laplacian growth, sandpiles and scaling limits surveys some of the advances.
- My senior thesis on the rotor-router model
was advised by Jim Propp.


- Confounding factors for
Hamilton's rule, the final paper for an anthropology class I took in
2002. I found that the rule is surprisingly
sensitive to changes in Hamilton's original hypotheses, which casts some
doubt on the evolutionary stability of kin selection.
- Hall's marriage theorem and Hamiltonian
cycles in graphs, the final paper from a spring 2001 reading course
with Richard Stanley.
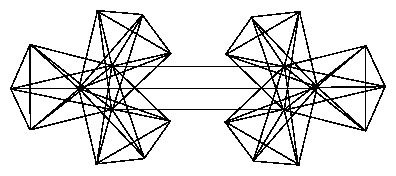
A graph on n=24 vertices having no Hamiltonian cycle, in which every set of k<22 vertices is adjacent to at least k+3 vertices:
- Some basic results on Sturmian
words, written before I knew that's what they were called. These
results are all known in some form. Theorem 1 and the surprising
corollary to Theorem 2 go back to Morse and Hedlund (1940).
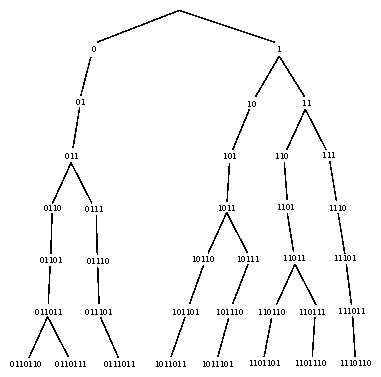
The beginning of the factor tree of the Sturmian word of slope sqrt(2)/2 and intercept zero: