Cox, Ross and Rubinstein developed the Binomial Model in 1979, which is also known as the CRR model. We will first present it through some examples before explaining the general case.

Example 1: One step model

Suppose that today €1=$1.5. Assume that you know that tomorrow the Euro will be worth either $1.2 with probability 1-p or $1.65 with probability p. Assume also that you can borrow or lend money in dollar currency at a fixed interest rate of 10%. Under these circumstances the market that you are facing can be modeled by a one step binomial model. One step because you are only given information about the Euro value tomorrow, binomial because there are only two possible values of the Euro tomorrow. The assumption that you can borrow or lend money at a fixed interest rate is a common assumption in short term financial models.

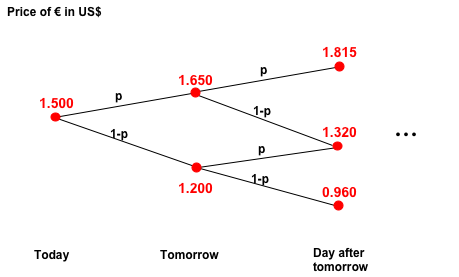
Example 2: Multistep Model

A natural generalization to the situation presented in the previous example arises when you face such a problem on a daily basis for a determined period of time. For example, suppose that today €1=$1.5 and for any given day of the month the probability of the price of the Euro to go down by 20% is 1-p while the probability of the price going up by 10% is p. As before assume that you can borrow or lend money at a fixed daily interest rate of 10%. In this case the market can be modeled by a multistep binomial model and the best way of visualizing such a model is through a binary tree like the one shown below.

The general case

The CRR model with time horizon T involves a riskless bond (which can be interpreted as a money market account or T-bonds) and a risky asset (e.g. stocks, bonds, commodities such as oil or gold, currency exchange rate, pork bellies etc.). The price process of the riskless bond is

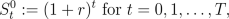
with r > -1. The price process of the risky asset is denoted by S_t for t=0,1,...,T where

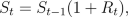
with R_t the return in the the tth trading period.. The return R_t can only take two possible values -1 < a < b. This implies that the price of the risky asset at any time t, either jumps to the higher value S_t (1+b) or to the lower value S_t (1+a).

Example 2 (continued)

We have in this case that the riskless bond is the dollar, the risky asset is the Euro, T is the number of days remaining in the month, r=0.1, a=-0.2 and b=0.1. Suppose further that you can borrow Euros with no interest, that p=0.5 and that there is only one day left in the month (so that you are facing a one step situation). You could take advantage of this circumstance by using the following strategy: borrow one Euro today, sell it immediately for $1.5 and lend this money (see Tangent). Tomorrow you will get for sure $1.65, since the interest rate is 10%. If the price of the Euro goes up to $1.65 you use your money to buy an Euro and pay your debt obtaining a net gain of $0. If the price of the Euro goes down to $1.2, you buy an Euro to pay your debt but in this case your ending balance is $1.65-$1.2=$0.45. Hence by following this strategy you can make $0.45 with a probability of 0.5 and no risk. Of course you could do the same with an arbitrary amount of Euros in the beginning, which generates even greater gains.

The situations presented in the previous examples give rise to the following question: under which circumstances is it possible to find a strategy to beat the market, in the sense that by following such strategy at time T you will have a positive profit with positive probability and no risk? We discuss this issue in the next lessons.