In the previous lessons we introduced
the Binomial Model. As we saw this model consists of one
riskless asset whose price changes over
time by a fixed
interest rate r and one risky asset
such that its
rate of return at any time can only take two possible values
a or b with
probabilities p and 1-p,
respectively. This rather simple structure prompted an
interesting question about conditions for the existence of
strategies to beat the market or
arbitrage opportunities. Regarding this issue we presented
the
First Fundamental Theorem of Asset Pricing reaching the
conclusion that if p is not 0 or 1 the market is
arbitrage-free if and only if a < r < b
.
In this section we will give a brief introduction
to the
concept of Financial Derivative. Financial Derivatives are
financial instruments used by investors to reduce the risk in the
market. These instruments give a more complex structure to
Financial Markets and elicit one of the main problems in
Mathematical Finance, namely to find fair prices for them. Under
more complicated models this question can be very hard but under
our binomial model is relatively easy to answer.
We say that y
depends linearly on
x1, x2,
..., xm if
y=a1x1+a2x2+
... +
amxm for some
constants
a1, a2,
..., am. Hence,
the payoff of a financial derivative is not of the
form
aS0+bS, with a
and b
constants.
Formally a Financial Derivative is a security
whose payoff
depends in a non-linear way on the primary assets,
S0 and S
in our model (see Tangent).
They are also called derivative securities and are
part of
a broarder cathegory known as contingent claims.
Contingent claims do not necessarily depend on the primary
assets. There exists a large number of derivative securities that
are traded in the market, below we present some of them.
Forward Contract
Under a forward contract, one agent agrees to sell to another
agent the risky asset at a future time for a price
K
which
is specified at time 0. The owner of a Forward Contract on the
risky asset
S with maturity
T
gains the difference
between the actual market price
ST
and the
delivery price K if
ST
is larger
than
K at time
T. If
ST
< k,
the owner loses the amount
K-ST
to the issuer
of the forward contract. Therefore, we can express the payoff of
Forward Contract by
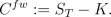
Call Option
The owner of a call option on the risky asset
S has
the
right, but no the obligation, to buy the asset at a future time
for a fixed price
K, called
strike
price.
When the owner has to exercise the option at maturity time the
option is called a
European Call Option. When the
owner
can choose the time to exercise his option it is known as an
American Call Option. The payoff of a
European Call Option
is of the form
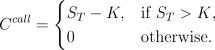
Put Option
Conversely, a put option gives the right, but no the obligation,
to sell the asset at a future time for a fixed price
K,
called
strike price. As before
when the owner has
to exercise the option at maturity time the option is called a
European Put Option. When the owner can
choose the time to
exercise his option it is known as an
American Put Option.
The payoff of a European Put Option is of the form
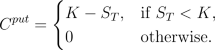
Remarks
We have seen in the previous examples that there are two
categories of options,
European type options and
American type options. This extends also
to financial
derivatives in general. The difference between the two is that
for European type derivatives the owner of the contract can only
"exercise" at a fixed maturity time whereas for American type
derivative the "exercise time" could occur before maturity.
In this section we will
concentrate our
attention on European type derivatives because they are
easier to price than American type derivatives.
There is a close relation between forwards and European call and
put options which is expressed in the following equation known as
the
put-call parity
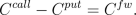
Hence, the payoff at maturity from buying a forward contract is
the same than the payoff from buying a European call option and
short selling a European put option.
Pricing
Once financial instruments like forwards and European call and
put options are defined the first question to answer is: what is
the
fair price that the seller of a Financial
Derivative
should charge to the buyer? In the previous lesson we have
developed the machinery necessary to answer this question. A fair
price of a European Type Derivative is the expectation of the
discounted final payoff with repect to a
risk-neutral
probability measure. These are fair prices because with them the
extended market in which the derivatives are traded assets is
arbitrage free (see
the
fundamental theorem of asset pricing).
In the arbitrage-free CRR model with p
strictly between
0 and 1 and a < r < b according to Acitvity
2 in the previous lesson we obtain the following prices for
forwards and European call and put options
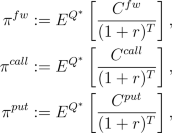
where,
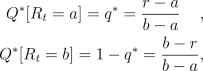
for any time
t. For instance, consider the market
given in
Example
3 but with
r=0. In this case
b=0.01
and
a=-0.03. The risk neutral measure is
given then by
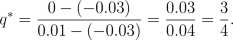
Consider a European call option with maturity of 2 days
(
T=2) and strike price
K=10*(0.97).
The risk
neutral measure and possible payoffs of this call option can be
included in the binary tree of the stock price as follows
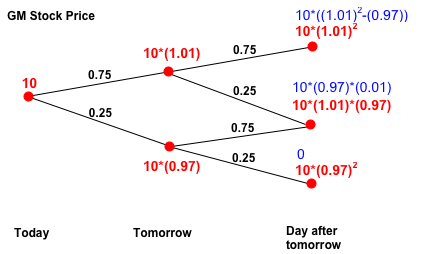
We find then that the price of this European call option is
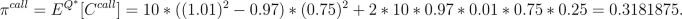
It is easy to see that the price of a forward contract with the
same maturity and same forward price
K is given by
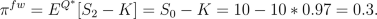
By the put-call parity mentioned above we deduce that the price
of an European put option with same maturity and same strike is
given by
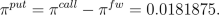
That the call option is more expensive than the put option is due
to the fact that in this market, the prices are more likely to go
up than down under the risk-neutral probability measure. This
does not happen if one considers the initial probabilities
p and
1-p.
Remark
Initially one is tempted to believe that for high values of
p the price of the call option should be
larger since it
is more certain that the price of the stock will go up. However
our arbitrage free argument leads to the same price for any
probability
p strictly between 0 and 1. How can
this be?
The best economical explanation is the following: If the
probability
p is almost one this reflects a change
in the
market participants risk aversion. Hence for large values of
p either the whole price structure
changes or the risk
aversion of the participants change and they value less any potential
gain and are more averse to any loss.
Activities
- A straddle
is a derivative whose payoff increases
proportionally to the change of the price of the risky asset.
Specifically, a straddle pays at time T the
difference between the price ST
and the price S0 if this
difference is positive and minus the difference if it is negative.
Basically with a straddle one is betting on the price move, regardless
of the direction of this move. Write down explicitely the payoff of a
straddle and find the price of a straddle with maturity T=2
for the model described above.
- Suppose that you want to buy
the text-book for your math finance class
in two days. Today the price of the book is $80 dollars. You know that
each day the price of the book goes up by 20% and down by 10% with the
same probability. Assume that you can borrow or lend money with no
interest rate. The bookstore offers you the option to buy the book the
day after tomorrow for $80. What is the fair fee the bookstore should
charge you for this option?
- Consider the same situation
than in b). Now the library offers you what
is called a discount certificate, you will receive
the smallest amount between the price of the book in two days and a
fixed quantity, say $80. What is the fair price of this contract?