Massive
short-selling is a practice that is often observed after the burst of a
price
bubble. Examples are the Dutch Tulip-mania in the seventeenth
century, the U.S. stock price crash in 1929, the NASDAQ price bubble of
1998-2000 and more recently the housing price bubble. Since the
practice of short-selling is alleged to magnify the decline of asset
prices, it has been banned and restricted many times during history. As
such, short-selling bans have been commonly used as a regulatory
measure to stabilize prices during downturns in the economy. The most
recent example was in September of 2008 with the prohibition of
short-selling by the U.S. Securities and Exchange Commission (SEC) for
799 financial companies in an effort to stabilize those companies. At
the same time the U.K. Financial Services Authority (FSA) prohibited
short selling for 32 financial companies. On September 22, Australia
enacted even more extensive measures with a total ban of short selling.
However, short-selling prohibition is not only seen after the burst of
a price bubble. In certain cases, the inability to short-sell is
inherent to the specific market. In the housing market, for example,
primary securities such as mortgages cannot be sold short. Additionally
in some of the developed markets and most of the emerging markets
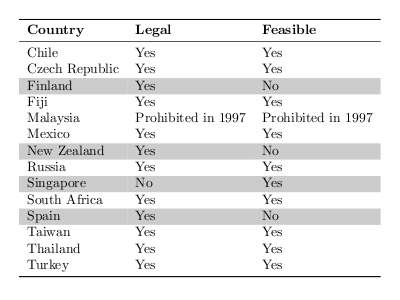
around the world short-selling securities is not feasible. In the table
below we highlighted, as of 2005, the developed markets were
short-selling is not feasible or illegal and listed the emerging
markets where short-selling is feasible. Also, in most of the examples
presented so far, the ability to short-sell the risky assets is crucial
in our arguments. In this section we will state the fundamental theorem
of asset pricing when the risky asset in the model cannot be sold short
and explore some of its consequences. In particular, we will see that
in this case the market is no longer complete.
Example: Dollar Vs Euro with short-selling
prohibition
The arbitrage opportunity presented in example 2 of
lesson
1 involves short-selling the Euro. Recall that in this
example the dollar's interest rate is 10% and the possible rates of
return of the risky asset are
d=-0.2 and
u=0.1.
Suppose now that the Euro cannot be sold short. One might ask then,
does there exist an arbitrage opportunity in
this market that does not sell the Euro short? In order to
answer this question we argue as follows. Suppose that
(x1,y1)
is a trading strategy (see
lesson
2) with nonpositive initial value, i.e.
x1+1.5y1≤0,
and
0≤y1 (this accounts for
the fact that the Euro cannot be sold short). The set of these
strategies can be represented by a cone in the plane (see figure
below). On the other hand the set of strategies that yield nonnegative
outcomes under both states of the world corresponds to strategies
(x1,y1),
such that
1.1x1+1.65y1≥0
and
1.1x1+1.2y1≥0.
These strategies can be represented by a cone in the plane as well (see
figure below).

The intersection of these cones is the strategy (0,0) which is not an
arbitrage opportunity (no strictly positive profit with positive
probability). We conclude then that prohibiting short-selling the Euro
makes this market arbitrage free.
Activity 1
- Consider example 3 of lesson
2 with time horizon equal to T=1. Arguing
as above, prove that if short-selling the GM stock is not allowed then
the market is arbitrage free.
- Can you find conditions on the
dollar's interest rate r
under which the market of part a) remains arbitrage free?
When
the
conditional
expectation under a probability
Q of a
process at a future time is less than or equal its present value, the
probability
Q is called a
supermartingale
measure. If the conditional expectation of the process at a
future time is greater than or equal its present value, the probability
Q is called a
submartingale
measure. A probability that is a supermartingale and a
submartingale measure simultaneously is a
martingale
measure.